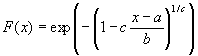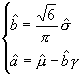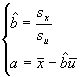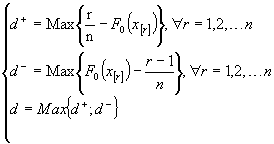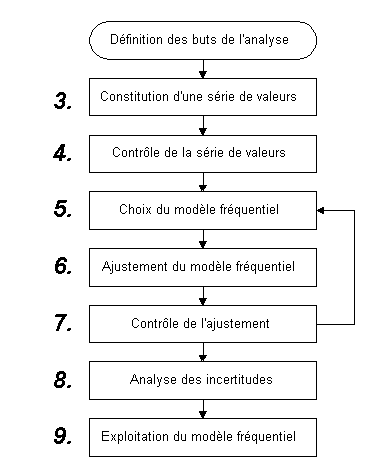
Principales étapes de l'analyse fréquentielle.
Ce sont essentiellement les étapes 5,6,7 et 8 qui sont développées dans ce document. Pour d'autres d'informations, prière de se référer au polycopié " Hydrologie fréquentielle, P. Meylan et A. Musy, EPFL, 1999 " duquel plusieurs graphiques de ce document ont été tirés.
Avant de commencer tout travail, il est primordial de formuler clairement les buts de l'analyse et d'adapter la démarche en conséquence. A cet égard, en hydrologie, l'un des critères essentiels est certainement l'échelle spatio-temporelle : étudier le comportement des crues dans un microbassin urbain (à très faible temps de concentration) avec des données de pluie au pas de temps mensuel n'aurait pas de sens ! L'inverse est tout aussi vrai : il est probablement inutile de disposer de pluies au pas de temps de la minute pour l'étude du bassin versant de l'Amazone !
La constitution d'échantillons, au sens statistique du terme, est un processus long, parsemé d'embûches, et au cours duquel de nombreuses erreurs, de nature fort différente, sont susceptibles d'être commises. Par ailleurs, il est indispensable, avant d'utiliser des séries de données, de se préoccuper de leur qualité et de leur représentativité. Le contrôle des données fera l'objet d'un chapitre qui sera traité ultérieurement dans ce cours.
A.2 Choix du modèle fréquentiel
La validité des résultats d'une analyse fréquentielle dépend du choix du modèle fréquentiel et plus particulièrement de son type. Diverses pistes peuvent contribuer à faciliter ce choix, mais il n'existe malheureusement pas de méthode universelle et infaillible.
A.2.1 Considérations théoriques
A.2.1.1 Loi normale
La loi normale se justifie, théoriquement par le théorème central-limite, comme la loi d'une variable aléatoire formée de la somme d'un grand nombre de variables aléatoires. En hydrologie fréquentielle des valeurs extrêmes, les distributions ne sont cependant pas symétriques, ce qui constitue un obstacle à son utilisation. Cette loi s'applique toutefois généralement bien à l'étude des modules annuels des variables hydro-météorologiques en climat tempéré.
A.2.1.2 Loi log-normale
La loi log-normale est préconisée
par certains hydrologues dont V.-T. Chow qui la justifient en argumentant
que l'apparition d'un événement hydrologique résulte
de l'action combinée d'un grand nombre de facteurs qui se multiplient.
Dès lors la variable aléatoire ![]() suit
une loi log-normale. En effet le produit de
suit
une loi log-normale. En effet le produit de ![]() variables
se ramène à la somme de
variables
se ramène à la somme de ![]() logarithmes
de celles-ci et le théorème central-limite permet d'affirmer
la log-normalité de la variable aléatoire.
logarithmes
de celles-ci et le théorème central-limite permet d'affirmer
la log-normalité de la variable aléatoire.
A.2.1..3 Loi de Gumbel
E.-J. Gumbel postule que la loi double exponentielle,
ou loi de Gumbel, est la forme limite de la distribution de la valeur maximale
d'un échantillon de ![]() valeurs.
Le maximum annuel d'une variable étant considéré comme
le maximum de 365 valeurs journalières, cette loi doit ainsi être
capable de décrire les séries de maxima annuels.
valeurs.
Le maximum annuel d'une variable étant considéré comme
le maximum de 365 valeurs journalières, cette loi doit ainsi être
capable de décrire les séries de maxima annuels.
Il est à remarquer que plus le nombre
de paramètres d'une loi est grand, plus l'incertitude dans l'estimation
est importante. Pratiquement il est par conséquent préférable
d'éviter l'utilisation de lois à trois paramètres ou
plus.
A.2.2 Comportement asymptotique
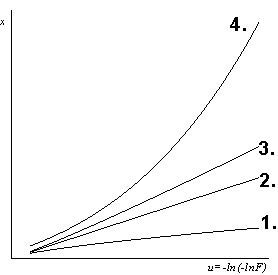
4 types de comportement asymptotique.
-
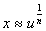 ,
avec n > 1, loi normale;
,
avec n > 1, loi normale; -
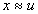 ,
croissance asymptotiquement exponentielle: loi de Gumbel, Pearson III,
loi des fuites;
,
croissance asymptotiquement exponentielle: loi de Gumbel, Pearson III,
loi des fuites; -
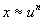 ,
avec n > 1: loi de Goodrich;
,
avec n > 1: loi de Goodrich; -
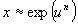 avec n > 0 (lois de type logarithme): loi log-normale (Galton),
Pearson V, Fréchet, log-gamma.
avec n > 0 (lois de type logarithme): loi log-normale (Galton),
Pearson V, Fréchet, log-gamma.
Cette approche suggère la plus grande prudence avec des lois de type
logarithmique qui peuvent largement surestimer les valeurs correspondant
à des fréquences rares.
A.2. 3 L'expérience et la coutume
Dans certains pays, ou dans certaines administrations, il existe en effet des règles ou normes qui fixent la méthodologie d'une analyse fréquentielle. Pour l'étude des débits maximums, par exemple, la loi log-Pearson III est recommandée aux Etats-Unis.
A.2.4 Utilisation des tests d'adéquation
A.2.5 Utilisation de divers diagrammes
A.2.5.1 Le diagramme des moments
Le diagramme de l'aplatissement ![]() en
fonction de la symétrie
en
fonction de la symétrie ![]() a
été introduit, semble-t-il, par K. Pearson à l'occasion
du développement de son système de lois de probabilité.
Le calcul de la symétrie
a
été introduit, semble-t-il, par K. Pearson à l'occasion
du développement de son système de lois de probabilité.
Le calcul de la symétrie ![]() et
de l'aplatissement
et
de l'aplatissement ![]() de
l'échantillon, puis le report du point figuratif dans le diagramme
de Pearson devrait donc permettre de faciliter le choix du modèle
à adopter. Il est cependant à remarquer que les courbes représentatives
des différentes lois utilisées en hydrologique sont relativement
confinées, ce qui rend une bonne différentiation assez difficile.
de
l'échantillon, puis le report du point figuratif dans le diagramme
de Pearson devrait donc permettre de faciliter le choix du modèle
à adopter. Il est cependant à remarquer que les courbes représentatives
des différentes lois utilisées en hydrologique sont relativement
confinées, ce qui rend une bonne différentiation assez difficile.
A.2.5.2 Le diagramme des L-moments
Les L-moments, en particulier le rapport ![]() qui
est une mesure de la symétrie et le rapport
qui
est une mesure de la symétrie et le rapport ![]() qui
est une mesure d'aplatissement, peuvent être utilisés dans
un diagramme analogue à celui de K. Pearson. La figure ci-dessous
illustre la position des lois fréquemment utilisées en hydrologie.
qui
est une mesure d'aplatissement, peuvent être utilisés dans
un diagramme analogue à celui de K. Pearson. La figure ci-dessous
illustre la position des lois fréquemment utilisées en hydrologie.
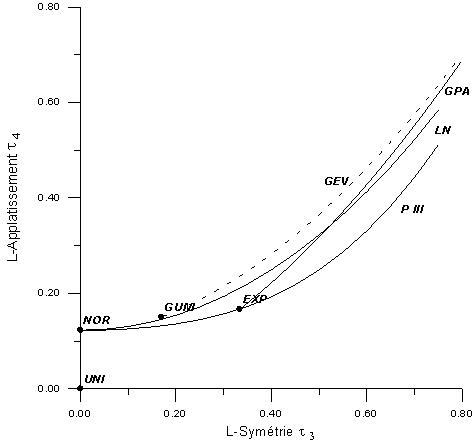
Diagramme des L-moments : symétrie ![]() -
aplatissement
-
aplatissement ![]() .
Les abréviations, désignant les lois, utilisées dans ce
diagramme sont les suivantes : UNI=uniforme, NOR=normale, GUM=Gumbel, EXP=exponentielle,
GEV=extrêmes généralisées, PIII=Pearson III, LN=log-normale,
GPA=Pareto généralisée.
.
Les abréviations, désignant les lois, utilisées dans ce
diagramme sont les suivantes : UNI=uniforme, NOR=normale, GUM=Gumbel, EXP=exponentielle,
GEV=extrêmes généralisées, PIII=Pearson III, LN=log-normale,
GPA=Pareto généralisée.
Il est à remarquer que dans ce graphique les lois à deux paramètres sont représentées comme un point, tandis que les lois à 3 paramètres sont figurées par une courbe.
A.3 Ajustement du modèle fréquentiel
Dans ce chapitre nous étudierons les techniques de l'ajustement ou du calage d'un modèle fréquentiel à une série de données : il s'agit de définir les paramètres de la loi retenue. Nous utiliserons comme support pédagogique la loi de Gumbel, fréquemment utilisée en hydrologie, pour modéliser les événements extrêmes, les pluies notamment.
A.3.1 Présentation de la loi de Gumbel
où ![]() est
le paramètre de position,
est
le paramètre de position, ![]() le
paramètre d'échelle et
le
paramètre d'échelle et ![]() le
paramètre de forme. 3 lois peuvent être distinguées en fonction
des valeurs de
le
paramètre de forme. 3 lois peuvent être distinguées en fonction
des valeurs de ![]() .
Leurs caractéristiques sont résumées dans le tableau suivant
:
.
Leurs caractéristiques sont résumées dans le tableau suivant
:
|
|
type
|
nom
|
borne inférieure
|
borne supérieure
|
|
|
III
|
|
|
|
|
|
I
|
Gumbel
|
|
+
|
|
|
II
|
Fréchet
|
|
|
La fonction de répartition de la loi de Gumbel s'exprime de la manière suivante :
Posons la variable réduite suivante ![]() .
La distribution s'écrit alors comme suit :
.
La distribution s'écrit alors comme suit : ![]() et
et ![]() .
L'avantage d'utiliser la variable réduite est que l'expression d'un
quantile est alors linéaire. En effet pour trouver la valeur
.
L'avantage d'utiliser la variable réduite est que l'expression d'un
quantile est alors linéaire. En effet pour trouver la valeur ![]() d'un
quantile, correspondant à la distribution
d'un
quantile, correspondant à la distribution ![]() ,
en fonction des deux paramètres
,
en fonction des deux paramètres ![]() et
et ![]() ,
il suffit d'utiliser la relation suivante :
,
il suffit d'utiliser la relation suivante :
![]()
A.3.2 Techniques d'ajustement
A.3.2.1 Méthode graphique
Dans le cas d'un ajustement selon la
loi de Gumbel, la méthode graphique repose sur le fait que l'expression
d'un quantile correspond à l'équation d'une droite. En conséquence,
les points de la série à ajuster peuvent être reportés
dans un système d'axes ![]() ;
il est alors possible de tracer la droite qui passe le mieux par ces points
et d'en déduire les deux paramètres
;
il est alors possible de tracer la droite qui passe le mieux par ces points
et d'en déduire les deux paramètres ![]() et
et ![]() définissant
la loi. Le graphique ci-dessous montre un ajustement à l'il. Dans
la mesure où les points
définissant
la loi. Le graphique ci-dessous montre un ajustement à l'il. Dans
la mesure où les points ![]() sont
connus (ils font partie de la donnée du problème), il suffit
de définir les coordonnées
sont
connus (ils font partie de la donnée du problème), il suffit
de définir les coordonnées ![]() correspondant
à chaque point pour pouvoir le positionner dans le graphique. Ces
coordonnées se déterminent à partir de la relation
inverse de la fonction de répartition qui donne
correspondant
à chaque point pour pouvoir le positionner dans le graphique. Ces
coordonnées se déterminent à partir de la relation
inverse de la fonction de répartition qui donne ![]() en
fonction de la distribution
en
fonction de la distribution ![]() .
Il s'agit donc essentiellement d'estimer la probabilité de non-dépassement
.
Il s'agit donc essentiellement d'estimer la probabilité de non-dépassement ![]() qu'il
convient d'attribuer à chaque valeur
qu'il
convient d'attribuer à chaque valeur ![]() .
.
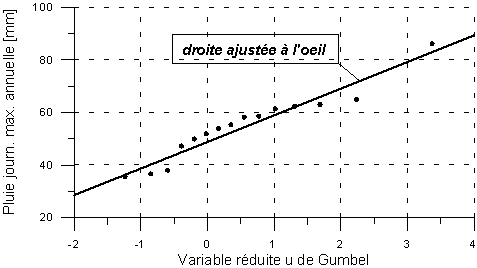
Principe de la méthode d'ajustement graphique.
Il existe de nombreuses formules d'estimation
de la fonction de répartition ![]() à
l'aide de la distribution empirique. Elles reposent toutes sur un tri
de la série par valeurs croissantes permettant d'associer à
chaque valeur son rang
à
l'aide de la distribution empirique. Elles reposent toutes sur un tri
de la série par valeurs croissantes permettant d'associer à
chaque valeur son rang ![]() .
Ces formules peuvent être résumées par une relation
générale qui garantit la symétrie autour de la
médiane :
.
Ces formules peuvent être résumées par une relation
générale qui garantit la symétrie autour de la
médiane :
où ![]() est
la taille de l'échantillon,
est
la taille de l'échantillon, ![]() la
valeur de rang
la
valeur de rang ![]() et
et ![]() un
coefficient compris entre 0 et 0.5. Le tableau ci-dessous présente quelques
exemples de distributions empiriques :
un
coefficient compris entre 0 et 0.5. Le tableau ci-dessous présente quelques
exemples de distributions empiriques :
| Nom | |
Formule |
| Weibull | |
|
| Cunnane | |
|
| Gringorten | |
|
| Hazen | |
|
Des simulations ont montré que pour la loi de Gumbel, il est judicieux utiliser la distribution empirique de Hazen
L'ajustement graphique, bien qu'étant une méthode approximative, a le très grand avantage de fournir une représentation visuelle des données et de l'ajustement. Celle-ci constitue un aspect essentiel du jugement porté sur l'adéquation entre la loi choisie et les données traitées, quelle que soit la méthode d'ajustement utilisée.
L'ajustement graphique est une approximation de la méthode statistique des moindres rectangles. Il est à remarquer cependant que, si un seul point parmi les données est fortement décalé par rapport aux autres, la méthode graphique est difficile à réaliser. En effet l'il humain a de la peine à juger le poids à donner à ce point. Dans ce cas, des méthodes statistiques rigoureuses doivent être utilisées.
A.3.2.2 Méthode des moments
La méthode des moments consiste
à égaler les moments échantillonnaux et les moments
théoriques de la loi choisie. Soit ![]() l'échantillon
de données à disposition. Posons
l'échantillon
de données à disposition. Posons ![]() et
et ![]() les
estimateurs standard de la moyenne et de la variance. Les deux premiers
moments théoriques de la loi de Gumbel s'expriment à partir
des paramètres de position et d'échelle de la manière
suivante :
les
estimateurs standard de la moyenne et de la variance. Les deux premiers
moments théoriques de la loi de Gumbel s'expriment à partir
des paramètres de position et d'échelle de la manière
suivante :
avec
(constante d'Euler).
On obtient donc les formules suivantes pour l'estimation par la méthode des moments :
A.3.2.3 Méthode des L-moments
Le but de cette méthode est
de réaliser un ajustement lorsque les moments classiques ne conviennent
pas. Les deux paramètres ![]() et
et ![]() sont
obtenus très simplement à partir des valeurs des deux
premiers L-moments de la loi de Gumbel et des estimations calculées
sur l'échantillon :
sont
obtenus très simplement à partir des valeurs des deux
premiers L-moments de la loi de Gumbel et des estimations calculées
sur l'échantillon :
avec
(constante d'Euler).
A.3.2.4 Méthode des moindres rectangles
La solution des moindres rectangles
conduit à trouver la droite bissectrice des solutions classiques
de la régression par moindres carrés de ![]() en
en ![]() d'une
part et de
d'une
part et de ![]() en
en ![]() d'autre
part. Cette méthode revient donc à minimiser la distance
du point à sa projection orthogonale sur la droite de régression.
Dans le cas de la loi de Gumbel l'axe
d'autre
part. Cette méthode revient donc à minimiser la distance
du point à sa projection orthogonale sur la droite de régression.
Dans le cas de la loi de Gumbel l'axe ![]() est
remplacé par l'axe
est
remplacé par l'axe ![]() de
la variable réduite de Gumbel et l'axe
de
la variable réduite de Gumbel et l'axe ![]() par
celui de la variable hydrologique étudiée que nous notons
ici
par
celui de la variable hydrologique étudiée que nous notons
ici ![]() .
.
Nous obtenons par cette méthode les estimateurs suivants :
A.3.2.5 Méthode du maximum de vraisemblance
La vraisemblance offre une approche
générale à l'estimation de paramètres inconnus
à l'aide de données. Soit ![]() un
échantillon provenant d'une loi
un
échantillon provenant d'une loi ![]() ,
où
,
où ![]() est
un paramètre inconnu qui peut être réel ou multivarié.
est
un paramètre inconnu qui peut être réel ou multivarié.
La fonction de vraisemblance, qu'il s'agit de maximiser, s'écrit :
où
est la densité de probabilité.
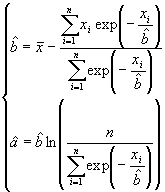
Souvent pour se simplifier le calcul, en remplaçant le produit par une somme, il est judicieux de maximiser le logarithme de la fonction de vraisemblance. On obtient dans le cas de la loi de Gumbel les estimateurs suivants :
La première équation doit être résolue de façon itérative. Dans ce cas la solution de la méthode des moments peut par exemple être utilisée comme première approximation.
Lorsque la taille de l'échantillon
est faible, la méthode du maximum de vraisemblance fournit une
estimation biaisée des paramètres. Il s'agit, dans ce
cas, d'utiliser la correction proposée par Fiorentino et Gabriele.
A.4 Contrôle de l'ajustement
A.4.1 Examen visuel de l'ajustement
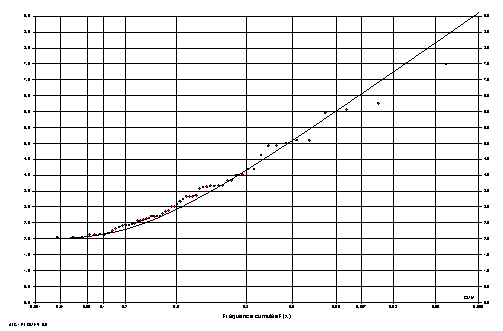
Ajustement de la série tronquée des débits de pointe [m3/s] du Nozon à Orny (1923-1931) à une loi exponentielle.
A.4.2 Le test chi-carré de K. Pearson
Pour tester l'adéquation d'une répartition théorique,
on dispose de deux éléments. D'une part, ![]() observations
réparties dans
observations
réparties dans ![]() cellules.
Cela se résume par :
cellules.
Cela se résume par :
| |
|
|
|
où ![]() est
le nombre d'observations dans la
est
le nombre d'observations dans la ![]() ème
cellule.
ème
cellule.
D'autre part, une distribution théorique qui fixe la probabilité ![]() (
(![]() )
de chaque cellule.
)
de chaque cellule.
| |
|
|
|
Le score du test de Pearson est une mesure de la distance entre
la répartition empirique et la loi théorique. Elle se base sur
la répartition des ![]() objets
selon la loi théorique :
objets
selon la loi théorique :
| |
|
|
|
Ensuite, on calcule :
L'hypothèse nulle que l'on teste
avec le test de Pearson est ![]() : " La distribution théorique est la vraie distribution sous-jacente
aux données ". On peut démontrer que : la distribution
de la statistique de Pearson sous l'hypothèse
: " La distribution théorique est la vraie distribution sous-jacente
aux données ". On peut démontrer que : la distribution
de la statistique de Pearson sous l'hypothèse ![]() est
bien approchée par une loi
est
bien approchée par une loi ![]() (chi-carré
avec
(chi-carré
avec ![]() degrés
de liberté), si le nombre espéré
degrés
de liberté), si le nombre espéré ![]() est
suffisamment grand (
est
suffisamment grand (![]() ).
).
On rejette donc l'hypothèse
nulle si ![]() où
où ![]() est
le 95%-quantile d'une loi
est
le 95%-quantile d'une loi![]() .
La figure ci-dessous illustre le principe de ce test.
.
La figure ci-dessous illustre le principe de ce test.
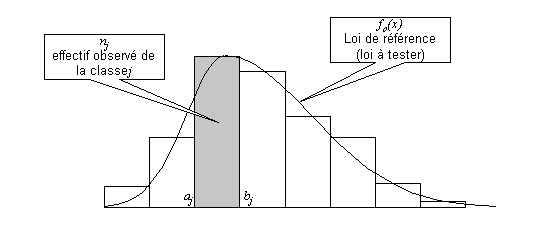
Principe du test de chi-carré.
Dans le cas où la variable aléatoire considérée est continue, il faut discrétiser, ce qui introduit un élément d'ambiguïté. Pour le cas continu il existe un autre test qui utilise la distribution empirique et qui, en règle générale, est plus puissant que le test de Pearson.
A.4.3 Le test de Kolmogorov-Smirnov
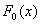 et
la distribution expérimentale
et
la distribution expérimentale On définit alors la statistique d comme suit :
La statistique ![]() est
tabulée dans plusieurs ouvrages. Le principe de ce test est
illustré dans la figure suivante :
est
tabulée dans plusieurs ouvrages. Le principe de ce test est
illustré dans la figure suivante :
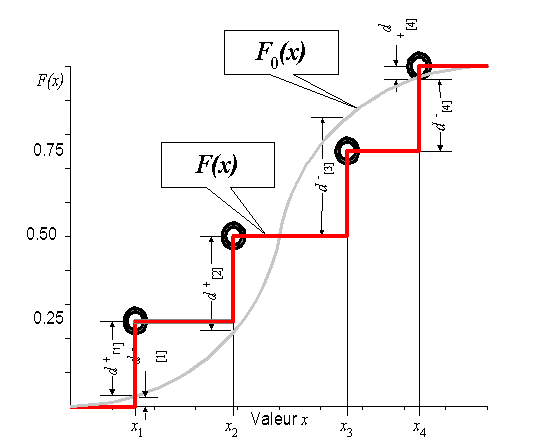
Principe du test de Kolmogorov-Smirnov.
A.4.4 Test d'AndersonDarling
Le test d'Anderson-Darling consiste à
comparer la distribution théorique ![]() à
la distribution expérimentale
à
la distribution expérimentale ![]() en
calculant la statistique suivante :
en
calculant la statistique suivante :
où ![]() est
une fonction de pondération.
est
une fonction de pondération.
Le cas standard d'Anderson-Darling correspond à la fonction de pondération suivante :
qui permet de donner plus d'influence
aux faibles et fortes fréquences. Cela conduit à la
statistique notée ![]() .
.
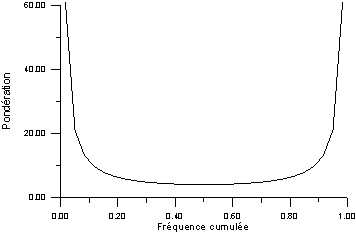
Fonction de pondération du test ![]() d'Anderson-Darling.
d'Anderson-Darling.
En modifiant la fonction de pondération en ![]()
on obtient un test sensible au
comportement pour des fréquences rares. Cette procédure
de test peut son se révéler particulièrement
utile lorsqu'on s'intéresse, comme c'est généralement
le cas en hydrologie, aux valeurs extrêmes.
A.5 Analyse des incertitudes
A ce stade de l'analyse nous disposons
d'un modèle fréquentiel ![]() ,
obtenu après plusieurs étapes. On est donc en droit
de se poser la question de sa fiabilité ou degré de
confiance que l'on peut y accorder.
,
obtenu après plusieurs étapes. On est donc en droit
de se poser la question de sa fiabilité ou degré de
confiance que l'on peut y accorder.
A.5.1 L'intervalle de confiance
Dans ce cas, la construction de l'intervalle de confiance nécessite la connaissance de trois grandeurs :
-
L'estimation du quantile, qui est donnée par l'équation
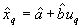 .
. -
L'erreur-type
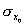 ,
dont la détermination sera développée ci-dessous.
,
dont la détermination sera développée ci-dessous. -
La forme de la distribution d'échantillonnage, considérée dans la plupart des cas comme " normale ".
A.5.1.1 Erreur-type d'un quantile
![]() Lorsque
les paramètres
Lorsque
les paramètres ![]() et
et ![]() de
la loi de Gumbel ont été estimés par la méthode
des moments l'expression d'un quantile
de
la loi de Gumbel ont été estimés par la méthode
des moments l'expression d'un quantile ![]() peut
s'écrire
peut
s'écrire ![]() .
En substituant les estimations de
.
En substituant les estimations de ![]() et
et ![]() ,
on obtient
,
on obtient
avec ![]() ,
constante d'Euler et
,
constante d'Euler et![]() est
appelé facteur de fréquence dans la formulation désormais
classique d'un quantile aux USA :
est
appelé facteur de fréquence dans la formulation désormais
classique d'un quantile aux USA :![]() .
.
En utilisant les formules de calcul
de la variance d'une fonction de variables aléatoires et
en remplaçant la variance ![]() par
son estimation
par
son estimation ![]() on
trouve finalement la formule de Dick et Darwin :
on
trouve finalement la formule de Dick et Darwin :
où en introduisant ![]() :
:
Lorsque les paramètres ont été estimés par la méthode du maximum de vraisemblance la procédure de calcul de l'erreur-type d'un quantile se base sur la méthode delta (méthode de linéarisation se basant sur le développement de Taylor). Pour la loi de Gumbel, on obtient :
Souvent la valeur de dimensionnement ![]() (ou
valeur de projet) à adopter est déterminée
à partir de l'erreur-type par une relation telle que celle
ci-:
(ou
valeur de projet) à adopter est déterminée
à partir de l'erreur-type par une relation telle que celle
ci-:
où ![]() est
un facteur, communément nommé facteur de fréquence,
dépendant de la forme de la loi de distribution d'échantillonnage
et du niveau de confiance
est
un facteur, communément nommé facteur de fréquence,
dépendant de la forme de la loi de distribution d'échantillonnage
et du niveau de confiance ![]() désiré.
Un tel intervalle de confiance est représenté par
la figure ci-dessous.
désiré.
Un tel intervalle de confiance est représenté par
la figure ci-dessous.
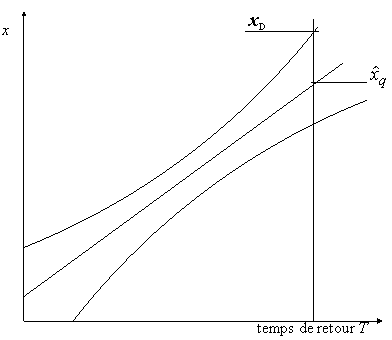
Intervalle de confiance à ![]() de
la valeur de dimensionnement.
de
la valeur de dimensionnement.
1) Ajuster la série des débits maximums annuels selon une distribution de Gumbel. Ajuster les données graphiquement.
2) Estimer les débits de pointe de temps de retour, 5, 20, 50, 100 ans.
3) Ajuster les données par la méthode des moments. Estimer les débits de pointe de temps de retour, 5, 20, 50, 100 ans.
Données :
L’exercice porte sur le bassin versant de la Mentue (station à Yvonand). Les données nécessaires à la réalisation de cet exercice se trouvent ci-dessous et dans un fichier Excel (il s’agit d’une série de débits maximums annuels en [m3/s] ).
1973 13.20
1972 15.40
1989 16.83
1975 18.09
1974 19.08
1976 20.81
1994 21.83
1971 23.00
1993 25.41
1981 27.59
1990 27.99
1987 29.65
1984 30.47
1978 30.82
1983 32.55
1980 33.25
1988 33.60
1986 35.47
1991 37.27
1985 37.43
1992 37.99
1977 41.50
1979 43.67
1995 45.40
1982 52.66
Réponse