 bassin versant représente, en principe,
l'unité géographique sur laquelle se base l'analyse du cycle hydrologique
et de ses effets.
bassin versant représente, en principe,
l'unité géographique sur laquelle se base l'analyse du cycle hydrologique
et de ses effets. Le  bassin versant représente, en principe,
l'unité géographique sur laquelle se base l'analyse du cycle hydrologique
et de ses effets.
bassin versant représente, en principe,
l'unité géographique sur laquelle se base l'analyse du cycle hydrologique
et de ses effets.
Plus précisément, le bassin versant qui peut être considéré comme un " système " est une surface élémentaire hydrologiquement close, c'est-à-dire qu'aucun écoulement n'y pénètre de l'extérieur et que tous les excédents de précipitations s'évaporent ou s'écoulent par une seule section à l'exutoire.
Le bassin versant en une section droite d'un cours d'eau, est donc défini comme la totalité de la surface topographique drainée par ce cours d'eau et ses affluents à l'amont de cette section. Il est entièrement caractérisé par son exutoire, à partir duquel nous pouvons tracer le point de départ et d'arrivée de la ligne de partage des eaux qui le délimite.
Généralement, la ligne de partage des eaux correspond à la ligne de crête. On parle alors de bassin versant topographique.
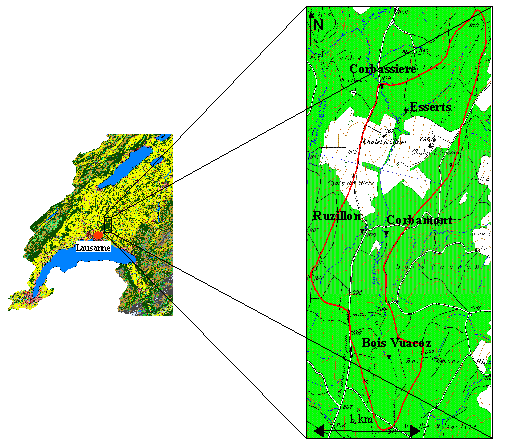
Fig. 2.1 - Bassin versant topographique de la Haute-Mentue (Suisse) et emplacements sous-bassins
Toutefois, la délimitation topographique nécessaire à la détermination en surface du bassin versant naturel n'est pas suffisante. Lorsqu'un sol perméable recouvre un substratum imperméable, la division des eaux selon la topographie ne correspond pas toujours à la ligne de partage effective des eaux souterraines (voir Fig. 2.2). Le bassin versant est alors différent du bassin versant délimité strictement par la topographie. Il est appelé dans ce cas bassin versant réel.
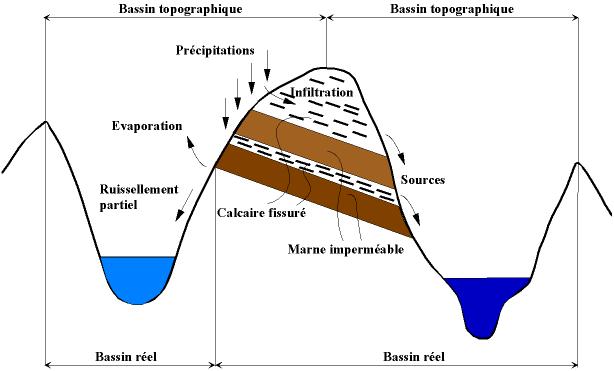
Fig. 2.2 - Distinction entre bassin
versant réel et bassin versant topographique
D'après Roche - Hydrologie de surface, Ed. Gauthier-Villars, Paris 1963.
Cette différence entre bassins réel et topographique est tout particulièrement importante en région karstique. Lorsque l'on s'intéresse au ruissellement, la délimitation du bassin versant doit aussi tenir compte des barrières artificielles (routes, chemins de fer, etc.). En effet, l'hydrologie du bassin versant, et notamment la surface drainée, peuvent être modifiées par la présence d'apports latéraux artificiels (réseaux d'eaux usées ou potables, drainages, routes, pompages ou dérivations artificielles modifiant le bilan hydrologique).
Fig. 2.3 - Exemples de modifications de la délimitation du bassin versant suite à la mise en place d'un réservoir et la construction d'une route
Il convient donc également de définir, en plus des délimitations topographiques, les limites souterraines de ce système. De plus, il est aussi nécessaire de tenir compte des effets anthropiques relatifs aux eaux du système.
L'analyse du comportement hydrologique d'un bassin
versant (système hydrologique) s'effectue le plus souvent par le biais de
l'étude de la réaction hydrologique du bassin face à une sollicitation (la
précipitation). Cette réaction est mesurée par l'observation de la
quantité d'eau qui s'écoule à l'exutoire du système. La représentation
graphique de l'évolution du débit Q en fonction du temps t
constitue un  hydrogramme de crue. La réaction du bassin
versant peut également être représentée par un
hydrogramme de crue. La réaction du bassin
versant peut également être représentée par un  limnigramme qui n'est autre que la
représentation de la hauteur d'eau mesurée en fonction du temps.
limnigramme qui n'est autre que la
représentation de la hauteur d'eau mesurée en fonction du temps.
La réaction hydrologique d'un bassin versant à une sollicitation particulière (Fig. 2.4) est caractérisée par sa vitesse (temps de montée tm, défini comme le temps qui s'écoule entre l'arrivée de la crue et le maximum de l'hydrogramme) et son intensité (débit de pointe Qmax, volume maximum Vmax, etc.). Ces deux caractéristiques sont fonction du type et de l'intensité de la précipitation qui le sollicite mais aussi d'une variable caractérisant l'état du bassin versant : le temps de concentration des eaux sur le bassin.
Fig. 2.4 - Principes d'analyse du comportement hydrologique du bassin versant et hydrogramme résultant.
La figure 2.5 fourni un exemple d'hydrogramme de crue
résultant d'un hyétogramme donné. Le  hyétogramme est la courbe représentant
l'intensité de la pluie en fonction du temps.
hyétogramme est la courbe représentant
l'intensité de la pluie en fonction du temps.
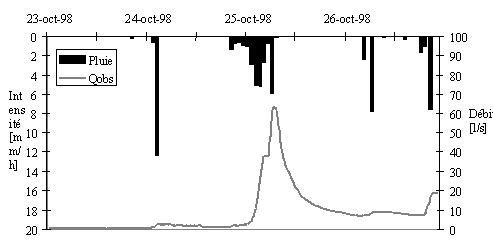
Fig. 2.5 - Exemple de réaction hydrologique pour le bassin versant de Bois-Vuacoz (Haute-Mentue)
 Le temps de concentration tc
des eaux sur un bassin versant se définit comme le maximum de durée
nécessaire à une goutte d'eau pour parcourir le chemin hydrologique entre
un point du bassin et l'exutoire de ce dernier.
Le temps de concentration tc
des eaux sur un bassin versant se définit comme le maximum de durée
nécessaire à une goutte d'eau pour parcourir le chemin hydrologique entre
un point du bassin et l'exutoire de ce dernier.
Il est composé de trois termes différents :
Le temps de concentration tc est donc égal au maximum de la somme de ces trois termes, soit :
| (2.1) |
Théoriquement on estime que tc est la durée comprise entre la fin de la pluie nette et la fin du ruissellement (cf. chapitre 11). Pratiquement le temps de concentration peut être déduit de mesures sur le terrain ou s'estimer à l'aide de formules le plus souvent empiriques.
Les courbes isochrones représentent les courbes d'égal temps de concentration des eaux sur le bassin versant. Ainsi, l'isochrone la plus éloignée de l'exutoire représente le temps mis pour que toute la surface du bassin versant contribue à l'écoulement à l'exutoire après une averse uniforme (Fig. 2.6). Le tracé du réseau des isochrones permet donc de comprendre en partie le comportement hydrologique d'un bassin versant et l'importance relative de chacun de ses sous-bassins.
Fig. 2.6 - Représentation d'un bassin
avec ses lignes isochrones et diagramme surface-temps de concentration
du bassin par élément de surface. On remarquera la forme des isochrones
au voisinage des éléments constitutifs
du réseau hydrographique.
Ces courbes permettent de déterminer, en faisant certaines hypothèses, l'hydrogramme de crue résultant d'une pluie tombée sur le bassin.
Les caractéristiques physiographiques d'un bassin versant influencent fortement sa réponse hydrologique, et notamment le régime des écoulements en période de crue ou d'étiage. Le temps de concentration tc qui, on l'a vu, caractérise en partie la vitesse et l'intensité de la réaction du bassin versant à une sollicitation des précipitations, est influencé par diverses caractéristiques morphologiques : en premier lieu, la taille du bassin (sa surface), sa forme, son élévation, sa pente et son orientation. A ces facteurs s'ajoutent encore le type de sol, le couvert végétal et les caractéristiques du réseau hydrographique. Ces facteurs, d'ordre purement géométrique ou physique, s'estiment aisément à partir de cartes adéquates ou en recourant à des techniques digitales et à des modèles numériques.
Le bassin versant étant l'aire de réception des précipitations et d'alimentation des cours d'eau, les débits vont être en partie reliés à sa surface.
La surface du bassin versant peut être mesurée par superposition d'une grille dessinée sur papier transparent, par l'utilisation d'un planimètre ou, mieux, par des techniques de digitalisation.
La forme d'un bassin versant influence l'allure de l'hydrogramme à l'exutoire du bassin versant. Par exemple, une forme allongée favorise, pour une même pluie, les faibles débits de pointe de crue, ceci en raison des temps d'acheminement de l'eau à l'exutoire plus importants. Ce phénomène est lié à la notion de temps de concentration.
En revanche, les bassins en forme d'éventail (bv1), présentant un temps de concentration plus court (tc1), auront les plus forts débits de pointe, comme le montre la figure suivante :
Fig. 2.7 - Influence de la forme du bassin versant sur l'hydrogramme de crue
Il existe différents indices morphologiques permettant de caractériser le milieu, mais aussi de comparer les bassins versants entre eux. Citons à titre d'exemple l'indice de compacité de Gravelius (1914) KG , défini comme le rapport du périmètre du bassin au périmètre du cercle ayant la même surface :
| (2.2) |
Avec :
KG est l'indice de compacité de Gravélius,
A : surface du bassin versant [km2],
P : périmètre du bassin [km].
Cet indice se détermine à partir d'une carte topographique en mesurant le périmètre du bassin versant et sa surface. Il est proche de 1 pour un bassin versant de forme quasiment circulaire et supérieur à 1 lorsque le bassin est de forme allongée, tel qu'illustré par la figure 2.8.
Fig. 2.8 - Exemples d'indices de compacité
L'influence du relief sur l'écoulement se conçoit aisément, car de nombreux paramètres hydrométéorologiques varient avec l'altitude (précipitations, températures, etc.) et la morphologie du bassin. En outre, la pente influe sur la vitesse d'écoulement. Le relief se détermine lui aussi au moyen d'indices ou de caractéristiques suivants :
La  courbe hypsométrique fournit une vue
synthétique de la pente du bassin, donc du relief. Cette courbe
représente la répartition de la surface du bassin versant en fonction de
son altitude. Elle porte en abscisse la surface (ou le pourcentage de
surface) du bassin qui se trouve au-dessus (ou au-dessous) de l'altitude
représentée en ordonnée (Fig. 2.9). Elle exprime ainsi la superficie du
bassin ou le pourcentage de superficie, au-delà d'une certaine altitude.
courbe hypsométrique fournit une vue
synthétique de la pente du bassin, donc du relief. Cette courbe
représente la répartition de la surface du bassin versant en fonction de
son altitude. Elle porte en abscisse la surface (ou le pourcentage de
surface) du bassin qui se trouve au-dessus (ou au-dessous) de l'altitude
représentée en ordonnée (Fig. 2.9). Elle exprime ainsi la superficie du
bassin ou le pourcentage de superficie, au-delà d'une certaine altitude.
Fig. 2.9 - Courbe hypsométrique du bassin versant de la Haute-Mentue
Ajoutons que lorsqu'on désire caractériser des bassins versants de haute montagne, on a l'habitude de tracer des courbes hypsométriques glaciaires, en planimétrant les surfaces recouvertes de glace.
Les courbes hypsométriques demeurent un outil pratique pour comparer plusieurs bassins entre eux ou les diverses sections d'un seul bassin. Elles peuvent en outre servir à la détermination de la pluie moyenne sur un bassin versant et donnent des indications quant au comportement hydrologique et hydraulique du bassin et de son système de drainage.
Elles sont obtenues directement à partir de cartes topographiques. L'altitude maximale représente le point le plus élevé du bassin tandis que l'altitude minimale considère le point le plus bas, généralement à l'exutoire. Ces deux données deviennent surtout importantes lors du développement de certaines relations faisant intervenir des variables climatologiques telles que la température, la précipitation et le couvert neigeux. Elles déterminent l'amplitude altimétrique du bassin versant et interviennent aussi dans le calcul de la pente.
L'altitude moyenne se déduit directement de la courbe hypsométrique ou de la lecture d'une carte topographique. On peut la définir comme suit :
| (2.3) |
Avec :
Hmoy : altitude moyenne du bassin [m] ;
Ai : aire comprise entre deux courbes de niveau [km2] ;
hi : altitude moyenne entre deux courbes de niveau [m] ;
A : superficie totale du bassin versant [km2].
L'altitude moyenne est peu représentative de la réalité. Toutefois, elle est parfois utilisée dans l'évaluation de certains paramètres hydrométéorologiques ou dans la mise en œuvre de modèles hydrologiques.
L'altitude médiane correspond à l'altitude lue au point d'abscisse 50% de la surface totale du bassin, sur la courbe hypsométrique. Cette grandeur se rapproche de l'altitude moyenne dans le cas où la courbe hypsométrique du bassin concerné présente une pente régulière.
La pente moyenne est une caractéristique importante qui renseigne sur la topographie du bassin. Elle est considérée comme une variable indépendante. Elle donne une bonne indication sur le temps de parcours du ruissellement direct - donc sur le temps de concentration tc - et influence directement le débit de pointe lors d'une averse.
Plusieurs méthodes ont été développées pour estimer la pente moyenne d'un bassin. Toutes se basent sur une lecture d'une carte topographique réelle ou approximative. La méthode proposée par Carlier et Leclerc (1964) consiste à calculer la moyenne pondérée des pentes de toutes les surfaces élémentaires comprises entre deux altitudes données. Une valeur approchée de la pente moyenne est alors donnée par la relation suivante :
| (2.4) |
Où :
im : pente moyenne[m/km ou 0/00],
L : longueur totale de courbes de niveau [km],
D : équidistance entre deux courbes de niveau [m],
A : surface du bassin versant [km2].
Cette méthode de calcul donne de bons résultats dans le cas d'un relief modéré et pour des courbes de niveau simples et uniformément espacées. Dans les autres cas, il convient de styliser les courbes de niveau pour que leur longueur totale ait un sens réel vis-à-vis de la pente.
Le calcul de la pente moyenne tout comme celui de leur exposition (orientation des pentes) peut-être assez facilement automatisée en se basant sur des données numériques représentant la topographie des bassins versants (Modèle Numérique d'Altitude). Le recours à ces données et méthodes et vivement encouragé. La dernière section de ce chapitre est consacrée aux informations digitales et aux modèles numériques.
Cet indice se calcule à partir du rectangle équivalent. Il est égal à la somme des racines carrées des pentes moyennes de chacun des éléments pondérés par la surface intéressée, soit :
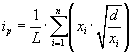 |
(2.5) |
où :
ip: indice de pente [%],
L: longueur du rectangle [m],
xi: distance qui sépare deux courbes sur la rectangle [m] (la largeur du rectangle étant constante, cette distance est égale au facteur de pondération),
d: distance entre 2 courbes de niveau successives (peut être variable) [m],
d/xi: pente moyenne d'un élément [%].
La notion de rectangle équivalent ou rectangle de Gravelius, introduite par Roche (1963), permet de comparer facilement des bassins versants entre eux, en ce qui concerne l'influence de leurs caractéristiques sur l'écoulement.
Le bassin versant rectangulaire résulte d'une transformation géométrique du bassin réel dans laquelle on conserve la même superficie, le même périmètre (ou le même coefficient de compacité) et donc par conséquent la même répartition hypsométrique. Les courbes de niveau deviennent des droites parallèles aux petits côtés du rectangle. La climatologie, la répartition des sols, la couverture végétale et la densité de drainage restent inchangées entre les courbes de niveau.
Si L et l représentent respectivement la longueur et la largeur du rectangle équivalent, alors :
Le périmètre du rectangle équivalent vaut : ![]() ;
la surface :
;
la surface :![]() ; le coefficient de compacité :
; le coefficient de compacité : ![]() .
.
En combinant ces trois relations, on obtient :
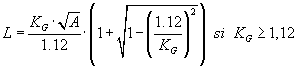 |
(2.6) |
Le tracé des droites de niveau du rectangle équivalent découle directement de la répartition hypsométrique cumulée.
Le  réseau hydrographique se définit comme
l'ensemble des cours d'eau naturels ou artificiels, permanents ou
temporaires, qui participent à l'écoulement. Le réseau hydrographique est
sans doute une des caractéristiques les plus importantes du bassin. Le
réseau hydrographique peut prendre une multitude de formes. La
différenciation du réseau hydrographique d'un bassin est due à quatre
facteurs principaux.
réseau hydrographique se définit comme
l'ensemble des cours d'eau naturels ou artificiels, permanents ou
temporaires, qui participent à l'écoulement. Le réseau hydrographique est
sans doute une des caractéristiques les plus importantes du bassin. Le
réseau hydrographique peut prendre une multitude de formes. La
différenciation du réseau hydrographique d'un bassin est due à quatre
facteurs principaux.
Afin de caractériser le réseau hydrographique, il est souvent utile de reporter son tracé en plan sur une carte à une échelle adéquate. L'utilisation de photographies analogiques ou numériques est utile à cette identification. Divers paramètres descriptifs sont utilisés pour définir le réseau hydrographique.
Par topologie, on entend l'étude des propriétés géométriques se conservant après déformations continues. Par extension, la topologie étudie les notions de voisinage et de limite. Appliquée à l'hydrologie, la topologie s'avère utile dans la description du réseau hydrographique notamment en proposant une classification de ceux-ci. A titre d'exemple, on trouve les types dendritique, en treillis, en parallèle, rectangulaire, à méandre, anastomosé, centripète, etc.
La classification est facilitée par un système de numérotation des tronçons de cours d'eau (rivière principale et affluents). L'ordre des cours d'eau est donc une classification qui reflète la ramification du cours d'eau. La codification des cours d'eau est également utilisée pour la codification des stations de mesures, permettant ainsi un traitement automatisé des données. Il existe plusieurs types de classifications des tronçons des cours d'eau, dont la classification de Strahler (1957) qui est la plus utilisée.
Cette classification permet de décrire sans ambiguïté le développement du réseau de drainage d'un bassin de l'amont vers l'aval. Elle se base sur les règles suivantes :
|
|
|
Fig. 2.10 - Classification du réseau hydrographique selon le système de Strahler (1957).
Un bassin versant a l'ordre du plus élevé de ses cours d'eau, soit l'ordre du cours d'eau principal à l'exutoire. Il existe d'autres classifications de ce type comme celle de Horton (1945) qui est parfois utilisée dans le même but.
Un bassin versant se caractérise principalement par les deux longueurs suivantes, illustrées sur la figure ci-dessous.
Fig. 2.11 - Longueurs caractéristiques d'un bassin versant, LCA : longueur du bassin versant ; L : longueur du cours d'eau principal
 profil longitudinal du cours
d'eau
profil longitudinal du cours
d'eauOn a l'habitude de représenter graphiquement la variation altimétrique du fond du cours d'eau en fonction de la distance à l'émissaire. Cette représentation devient intéressante lorsque l'on reporte les cours d'eau secondaires d'un bassin versant qu'il est alors facile de comparer entre eux et au cours d'eau principal. Notons qu'il est d'usage d'utiliser un graphisme différent lorsque les affluents sont en rive gauche ou droite de la rivière dont ils sont tributaires. Le profil en long d'un cours d'eau permet de définir sa pente moyenne.
Fig. 2.12 - Profil en long de la Broye avec représentation de ses affluents (D'après Parriaux : Contribution à l'étude des ressources en eau du bassin de la Broye)
La pente moyenne du cours d'eau détermine la vitesse avec
laquelle l'eau se rend à l'exutoire du bassin donc le temps de
concentration. Cette variable influence donc le débit maximal observé. Une
pente abrupte favorise et accélère l'écoulement superficiel, tandis qu'une
pente douce ou nulle donne à l'eau le temps de s'infiltrer, entièrement ou
en partie, dans le sol.
Le calcul des pentes moyennes et partielles de cours d'eau s'effectue à
partir du profil longitudinal du cours d'eau principal et de ses
affluents. La méthode la plus fréquemment utilisée pour calculer la pente
longitudinale du cours d'eau consiste à diviser la différence d'altitude
entre les points extrêmes du profil par la longueur totale du cours d'eau.
| (2.7) |
Où :
Pmoy : pente moyenne du cours d'eau [m/km] ;
DHmax : dénivellation maximale de la rivière [m] (différence d'altitude entre le point le plus éloigné et l'émissaire) ;
L : longueur du cours d'eau principal [km].
On préférera parfois utiliser d'autres méthodes plus représentatives : par exemple celle qui consiste à assimiler la pente moyenne à la pente de la droite tracée entre les points situés à 15% et 90% de distance à partir de l'exutoire, suivant le cours d'eau principal (Benson, 1959) ; ou encore, comme le préconise Linsley (1982), on prendra la pente de la ligne, tracée depuis l'exutoire, dont la surface délimitée est identique à la surface sous le profil en long (Fig. 2.13).
Fig. 2.13 - Calcul de la pente moyenne du cours d'eau selon Linsley (1982)
A partir de données sur un bon nombre de bassins versants (Hack, 1957), une relation a pu être établie entre la longueur L [km] de la rivière et l'aire A [km2] du bassin versant :
| (2.8) |
On peut aussi définir la courbe aire-distance, qui met en relation la longueur moyenne des cours d'eau d'ordre u donné et l'aire tributaire moyenne des cours d'eau du même ordre u, et ceci ordre par ordre. Cette courbe permet de visualiser la répartition des superficies du bassin par rapport à l'exutoire ou par rapport au point de mesure du débit. Cette répartition affecte en effet la concentration du ruissellement et donc influence la réponse hydrologique du bassin versant.
 densité de drainage
densité de drainageLa densité de drainage, introduite par Horton, est la longueur totale du réseau hydrographique par unité de surface du bassin versant :
| (2.9) |
Avec :
Dd : densité de drainage [km/km2] ;
Li : longueur de cours d'eau [km] ;
A : surface du bassin versant [km2].
La densité de drainage dépend de la géologie (structure et lithologie) des caractéristiques topographiques du bassin versant et, dans une certaine mesure, des conditions climatologiques et anthropiques. En pratique, les valeurs de densité de drainage varient de 3 à 4 pour des régions où l'écoulement n'a atteint qu'un développement très limité et se trouve centralisé ; elles dépassent 1000 pour certaines zones où l'écoulement est très ramifié avec peu d'infiltration. Selon Schumm, la valeur inverse de la densité de drainage, C=1/Dd, s'appelle « constante de stabilité du cours d'eau ». Physiquement, elle représente la surface du bassin nécessaire pour maintenir des conditions hydrologiques stables dans un vecteur hydrographique unitaire (section du réseau).
La densité hydrographique représente le nombre de canaux d'écoulement par unité de surface.
| (2.10) |
Où :
F : densité hydrographique [km-2] ;
Ni : nombre de cours d'eau ;
A : superficie du bassin [km2].
Il existe une relation assez stable entre la densité de drainage Dd et la densité hydrographique F, de la forme :
| (2.11) |
Où a est un coefficient d'ajustement.
En somme, les régions à haute densité de drainage et à haute densité hydrographique (deux facteurs allant souvent de pair) présentent en général une roche mère imperméable, un couvert végétal restreint et un relief montagneux. L'opposé, c'est-à-dire faible densité de drainage et faible densité hydrographique, se rencontre en région à substratum très perméable, à couvert végétal important et à relief peu accentué.
Sur la base de la classification des cours d'eau, Horton (1932) et Schumm (1956) ont établi différentes lois :
| Loi des nombres : |
(2.12) |
| Loi des longueurs : |
(2.13) |
| Loi des aires : |
(2.14) |
Avec :
RB : rapport de confluence des cours d'eau ("bifurcation ratio") ;
RL : rapport des longueurs des cours d'eau ; RA : rapport des aires des cours d'eau ;
u : ordre d'un cours d'eau u varie entre 1 et w (w est l'ordre du cours d'eau principal, classification selon Strahler) ;
Nu : nombre des cours d'eau d'ordre u ; Nu+1 : nombre des cours d'eau d'ordre suivant ;
Lu : longueur moyenne des cours d'eau d'ordre u ;
Au : aire tributaire moyenne des cours d'eau d'ordre u.
Le  rapport de confluence est un nombre sans
dimension exprimant le développement du réseau de drainage. Il varie
suivant l'ordre considéré. C'est un élément important à considérer pour
établir des corrélations d'une région à une autre. Selon Strahler (1964),
le RB varie de 3 à 5 pour une région où la géologie n'a aucune
influence. La réponse hydrologique de différents types de bassins est
illustrée sur la figure 2.14. On remarque que le rapport de confluence le
plus élevé est rencontré sur le bassin de forme le plus allongé et
présentant une vallée étroite et pentue (bassin A). Pour le bassin C, la
valeur RB est la valeur moyenne du rapport de
confluence déterminée grâce à la pente (valeur absolue) de la régression
entre le logarithme en base 10 de Nu (ordonnée) et les
ordres des cours d'eau u (abscisse).
rapport de confluence est un nombre sans
dimension exprimant le développement du réseau de drainage. Il varie
suivant l'ordre considéré. C'est un élément important à considérer pour
établir des corrélations d'une région à une autre. Selon Strahler (1964),
le RB varie de 3 à 5 pour une région où la géologie n'a aucune
influence. La réponse hydrologique de différents types de bassins est
illustrée sur la figure 2.14. On remarque que le rapport de confluence le
plus élevé est rencontré sur le bassin de forme le plus allongé et
présentant une vallée étroite et pentue (bassin A). Pour le bassin C, la
valeur RB est la valeur moyenne du rapport de
confluence déterminée grâce à la pente (valeur absolue) de la régression
entre le logarithme en base 10 de Nu (ordonnée) et les
ordres des cours d'eau u (abscisse).
Fig. 2.14 - Bassins versants hypothétiques de différents rapports de confluence RB et schématisation des hydrogrammes correspondant. D'après Chow, Handbook of applied hydrology, Mc Graw-Hill, 1964.
L' endoréisme est un phénomène rencontré dans
certains bassins versants pour lesquels le réseau hydrographique n'est
relié à aucun autre réseau. L'eau est alors acheminée et concentrée en un
point du bassin qui peut être un lac, une mare ou une accumulation
souterraine. Ce phénomène est généralement observé en zones arides (ex :
mare d'Oursi au Burkina Faso, lac Tchad, mer Morte, etc.).
endoréisme est un phénomène rencontré dans
certains bassins versants pour lesquels le réseau hydrographique n'est
relié à aucun autre réseau. L'eau est alors acheminée et concentrée en un
point du bassin qui peut être un lac, une mare ou une accumulation
souterraine. Ce phénomène est généralement observé en zones arides (ex :
mare d'Oursi au Burkina Faso, lac Tchad, mer Morte, etc.).
L'activité végétative et le type de sol sont intimement liés et leurs actions combinées influencent singulièrement l'écoulement en surface. Le couvert végétal retient, selon sa densité, sa nature et l'importance de la précipitation, une proportion variable de l'eau atmosphérique. Cette eau d'interception est en partie soustraite à l'écoulement.
La forêt, par exemple, intercepte une partie de l'averse par sa frondaison. Elle exerce une action limitatrice importante sur le ruissellement superficiel. La forêt régularise le débit des cours d'eau et amortit les crues de faibles et moyennes amplitudes. Par contre, son action sur les débits extrêmes causés par des crues catastrophiques est réduite.
A l'inverse, le sol nu, de faible capacité de rétention favorise un ruissellement très rapide. L'érosion de la terre va généralement de paire avec l'absence de couverture végétale.
Etant donné l'importance du rôle joué par la forêt, on traduit parfois sa présence par un indice de couverture forestière K :
| (2.15) |
On peut calculer ce type d'indice avec d'autres couvertures végétales telle que les cultures.
Parmi les éléments de la couverture du sol qui influencent le comportement hydrologique d'un bassin versant, on doit prendre en compte la présence de surfaces d'eau libre tels que les lacs qui jouent un rôle important du fait de leur capacité de stockage temporaire d'un certain volume d'eau. Ce stockage temporaire a ainsi pour effet de laminer les crue c'est à dire de réduire le débit de pointe de la crue. Cet effet de laminage est illustré pour le Rhône (entre son entrée dans le Léman au niveau de la Porte du Scex et sa sortie à Genève) dans la figure 2.15 dans laquelle on a représenté les valeurs du coefficient mensuel de débit (rapport entre le débit mensuel et la moyenne annuelle des débits sur une longue période de mesure).
Un indice analogue à celui de la couverture forestière peut-être identifié pour quantifier l'importance de ces plans d'eau.
On soulignera encore que la surface du cours d'eau constitue aussi un plan d'eau et que le canal d'une rivière permet aussi de laminer une crue.
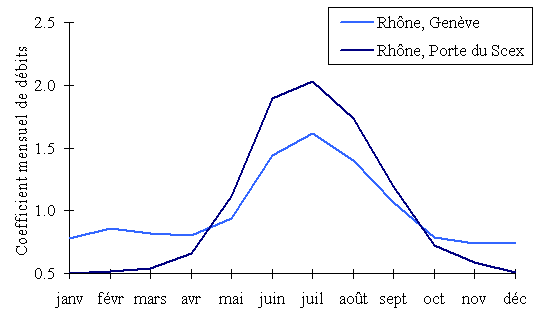
Fig. 2.15 - Illustration de l'effet de laminage par un plan d'eau. Le cas du Léman sur le débit du Rhône
Certains bassins d'altitude peuvent être partiellement ou
totalement couvert de neige ou de glace. Ce type de couverture doit être
pris en compte dans l'étude des facteurs de génération de l'écoulement de
l'eau. En effet, le réchauffement printanier de la température peut
entraîner une fonte rapide de la neige et provoquer du même coup un
important écoulement d'eau venant s'ajouter à celui de l'eau des
précipitations. De la même manière, la présence de glaciers ou le gel des
cours d'eau durant l'hiver peut, lors des processus de fonte, générer des
crues de  débâcle de glace se traduisant par un
transport de blocs de glace. Ceux-ci peuvent localement bloquer
l'écoulement de l'eau (
débâcle de glace se traduisant par un
transport de blocs de glace. Ceux-ci peuvent localement bloquer
l'écoulement de l'eau ( embâcle) jusqu'à la rupture de ces barrages
naturels. Il s'ensuit alors des crues rapides et intenses pouvant avoir
des conséquences catastrophiques.
embâcle) jusqu'à la rupture de ces barrages
naturels. Il s'ensuit alors des crues rapides et intenses pouvant avoir
des conséquences catastrophiques.
Il est toujours possible de calculer un indice analogue à celui de la couverture forestière pour les surfaces enneigées et celles des glaciers.
Les surfaces imperméables jouent un très grand rôle en hydrologie urbaine. Elles augmentent l'écoulement de surface, réduisent les infiltrations et la recharge des nappes, et diminuent le temps de concentration. On calcule souvent un taux d'imperméabilité qui est le rapport entre les surfaces imperméables et la surface totale.
Pour caractériser la capacité d'un bassin versant à ruisseler un indice est très souvent utilisé en hydrologie de surface : le coefficient de ruissellement (Cr). Son calcul et son emploi sont simples, mais notons qu'il peut conduire à commettre de grossières erreurs. Ce coefficient est défini comme suit :
| (2.16) |
Ce coefficient est fortement influencé par la couverture du sol comme le montre le tableau suivant dans lequel les quelques valeurs de ce coefficient issues des normes suisses SNV sont présentées. Ces valeurs reflètent la capacité des sols à ruisseler en fonction uniquement de la couverture du sol. On remarque notamment le très fort taux du coefficient de ruissellement donné pour les routes et toitures. Comme on l'a vu, cela s'explique par le fait que ces surfaces sont pratiquement imperméables.
Tableau 2.1 Valeurs du coefficient de
ruissellement pour différentes couvertures du sol
(Tiré des normes suisses SNV 640 351)
|
Nature superficielle du bassin versant |
Coefficient de ruissellement Cr |
|
Bois |
0,1 |
|
Prés, champs cultivés |
0,2 |
|
Vignes, terrains nus |
0,5 |
|
Rochers |
0,7 |
|
Routes sans revêtement |
0,7 |
|
Routes avec revêtement |
0,9 |
|
Villages, toitures |
0,9 |
La nature du sol intervient sur la rapidité de montée des crues et sur leur volume. En effet, le taux d'infiltration, le taux d'humidité, la capacité de rétention, les pertes initiales, le coefficient de ruissellement (Cr) sont fonction du type de sol et de son épaisseur.
Pour étudier ce type de réactions, on peut comparer le coefficient de ruissellement sur différentes natures de sol (intérêt d'une carte pédologique détaillée dans les études de prédétermination des crues). La littérature fournit des valeurs du coefficient de ruissellement pour chaque type de sol et, très souvent, en rapport avec d'autres facteurs tels que la couverture végétale, la pente du terrain ou l'utilisation du sol. Un exemple est donné dans le tableau 2.2 pour la Suisse, et en secteur rural.
Tableau 2.2 Différentes valeurs de coefficient de ruissellement pour les cas suisses. Cr est une fonction de la pente et de la couverture du sol. (Tiré de Sautier, Guide du Service Fédéral des Améliorations foncières)
|
|
Couverture du sol |
||
|
Pente % |
Forêts |
Pré-champ |
Culture dans la sens de la pente |
|
0,5 |
-- |
0,005 |
0,12 |
|
1,0 |
0,01 |
0,020 |
0,13 |
|
2,0 |
0,02 |
0,040 |
0,18 |
|
4,0 |
0,04 |
0,070 |
0,23 |
|
6,0 |
0,05 |
0,090 |
0,27 |
|
8,0 |
0,06 |
0,110 |
0,31 |
|
10,0 |
0,07 |
0,130 |
0,34 |
|
15,0 |
0,08 |
0,170 |
0,40 |
|
20,0 |
0,10 |
0,190 |
0,45 |
|
25,0 |
0,12 |
0,220 |
0,50 |
|
30,0 |
0,13 |
0,250 |
0,55 |
|
35,0 |
0,14 |
0,270 |
0,59 |
|
40,0 |
0,15 |
0,290 |
0,62 |
|
45,0 |
0,16 |
0,310 |
0,65 |
|
50,0 |
0,17 |
0,330 |
0,69 |
On peut introduire, dès à présent, une caractéristique du
sol importante : l'état d'humidité du sol qui est un des
facteurs principaux conditionnant les temps de concentration. Cet état est
cependant très difficile à mesurer car très variable dans l'espace et le
temps. On a souvent recours à d'autres paramètres qui reflètent l'humidité
du sol et qui sont plus faciles à obtenir. En hydrologie, on fait
souvent appel à des indices caractérisant les conditions d'humidité
antécédentes à une pluie. Il en existe de nombreux qui sont pour la
plupart basés sur les précipitations tombées au cours d'une certaine
période précédant un événement. Ils sont généralement notés IPA,
c'est-à-dire  Indices de Précipitations Antécédentes (API
en anglais).
Indices de Précipitations Antécédentes (API
en anglais).
La forme la plus classique de cet indice repose sur le principe de décroissance logarithmique avec le temps du taux d'humidité du sol, au cours des périodes sans précipitations :
| (2.17) |
Avec :
IPA0 : valeur initiale de l'indice des précipitations antécédentes [mm] ;
IPAt : valeur de cet indice t jours plus tard [mm] ;
K : facteur de récession, K< 1. Il est variable d'un bassin à l'autre, ainsi que d'une saison à l'autre pour un même bassin ;
t : temps [jour].
L'Institut d'Aménagement des Terres et des Eaux de l'EPFL (IATE/HYDRAM), après différents travaux de recherche sur parcelles expérimentales, a adopté un indice de la forme suivante :
| (2.18) |
Où :
IPAi : indice de précipitations antérieures au jour i [mm] ;
IPAi-1 : indice de pluies antécédentes au jour i-1 [mm] ;
Pi-1 : précipitations tombées au jour i-1 [mm] ;
K : coefficient inférieur à 1, en général compris entre 0,8 et 0,9.
La figure 2.16 illustre le calcul de l'IPA au cours d'une année à la station de Payerne (VD).
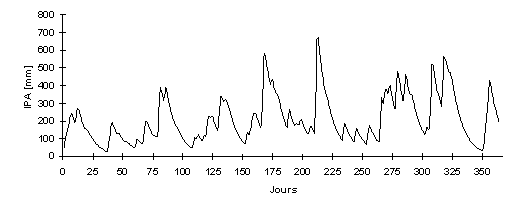
Fig. 2.16 - Variation de l'indice IPA en fonction du temps à Payerne (VD) en 1991 (K = 0.9).
La connaissance de la géologie d'un bassin versant
s'avère importante pour cerner l'influence des caractéristiques
physiographiques. La géologie du substratum influe non seulement sur
l'écoulement de l'eau souterraine mais également sur le ruissellement de
surface. Dans ce dernier cas, les caractères géologiques principaux à
considérer sont la lithologie (nature de la roche mère) et la structure
tectonique du substratum. L'étude géologique d'un bassin versant dans le
cadre d'un projet hydrologique a surtout pour objet de déterminer la
perméabilité du substratum. Celle-ci intervient sur la vitesse de montée
des crues, sur leur volume et sur le soutien apporté aux  débits d'étiage par les nappes
souterraines. Un bassin à substratum imperméable présente une crue plus
rapide et plus violente qu'un bassin à substratum perméable, soumis à une
même averse. Ce dernier retient l'eau plus aisément, et en période de
sécheresse, un
débits d'étiage par les nappes
souterraines. Un bassin à substratum imperméable présente une crue plus
rapide et plus violente qu'un bassin à substratum perméable, soumis à une
même averse. Ce dernier retient l'eau plus aisément, et en période de
sécheresse, un  débit de base sera ainsi assuré plus
longtemps. Néanmoins, le substratum peut absorber une certaine quantité
d'eau dans les fissures et diaclases des roches naturellement imperméables
ou dans les formations rocheuses altérées.
débit de base sera ainsi assuré plus
longtemps. Néanmoins, le substratum peut absorber une certaine quantité
d'eau dans les fissures et diaclases des roches naturellement imperméables
ou dans les formations rocheuses altérées.
Pour ces dernières, la dissolution de certains éléments et leur migration, menant à la formation de canaux, peut créer une circulation souterraine importante. Ce phénomène se retrouve sans exception dans les régions karstiques. Dans ce cas, l'étude géologique devra être beaucoup plus détaillée de manière à localiser les nappes d'eaux souterraines, leur zone d'alimentation et leurs résurgences. Cette étude devra être réalisée par un hydrogéologue.
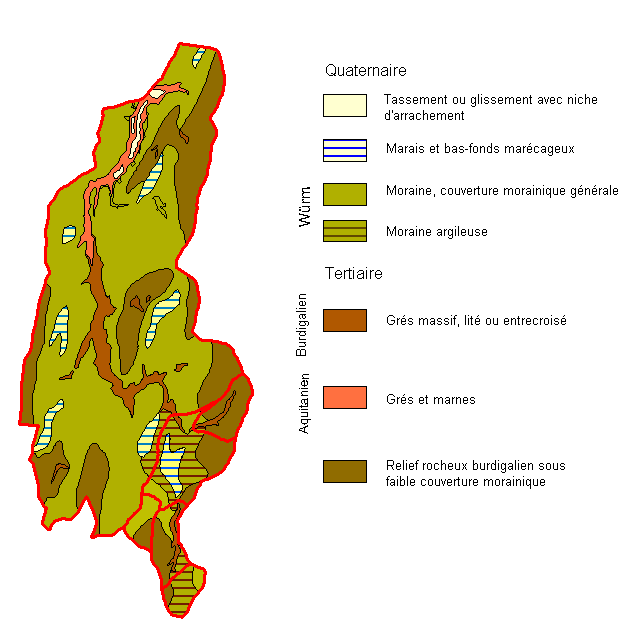
Fig. 2.17 - Carte géologique du bassin versant de la Haute-Mentue
La demande de données spatiales s'est accrue ces dernières années car l'on sait désormais qu'il est essentiel de connaître la distribution spatiale de la réponse hydrologique pour bien comprendre les processus sous-jacents de la génération de l'écoulement. De plus, la représentation et la connaissance du terrain sont essentielles pour comprendre les processus d'érosion, de sédimentation, de salinisation et de pollution via des cartes de risque.
Aujourd'hui, le développement de techniques modernes d'acquisition et de mise à disposition d'informations digitales a rendu possible la représentation à la fois de la topographie du milieu par le biais de modèles numériques d'altitude (MNA) et de terrain (MNT) ainsi que la représentation de l'occupation des sols par le biais de photographies aériennes ou de données satellitaires. Ces informations servent de plus en plus à la description des caractéristiques physiques des bassins versants et à la cartographie numérique de leur couverture.
Nous n'aborderons ici que les modèles numériques d'altitude (MNA) et de terrain (MNT).
A partir de la densité locale de courbes de niveau ou de traitement stéréoscopique d'images satellitaires, il est possible de produire une spatialisation du milieu (MNA) qui, in fine, aboutit à l'élaboration de modèles numériques de terrain (MNT). Ce MNT est une expression numérique de la topographie, sous forme matricielle ou vectorielle. Outre les altitudes (MNA), les fichiers qui le constituent sont les pentes, l'orientation et l'éclairage simulé.
Schématiquement, on distingue trois types essentiels de découpage spatial du milieu utilisés pour la génération d'un MNA. Il s'agit respectivement de :
A partir de ces trois approches, il est possible de déterminer plusieurs attributs du modèle numérique d'altitude tels que des attributs topographiques (élévation, orientation, pente, surface, courbure) qui influencent diverses grandeurs intervenant directement dans les processus d'écoulement.
En Suisse, le nouveau modèle numérique du terrain MNT25 est disponible pour toute la superficie du pays depuis fin 1996 (http://https://shop.swisstopo.admin.ch/fr/products/height_models/dhm25200). Ce modèle est établi à partir de la digitalisation des courbes de niveaux des feuilles topographiques à l'échelle 1:25'000. Dans une seconde étape, le modèle matriciel du MNT25 est interpolé avec une maille de 25 m. Ce jeu de données est uniquement destiné à l'emploi numérique. Il répond aux exigences demandées pour des applications d'une très grande précision. La précision altimétrique du MNT25 est d'environ 1,5 m sur le Plateau, entre 5 et 8 m dans les Alpes.