

Sont dénommées précipitations, toutes les eaux météoriques qui tombent sur la surface de la terre, tant sous forme liquide (bruine, pluie, averse) que sous forme solide (neige, grésil, grêle) et les précipitations déposées ou occultes (rosée, gelée blanche, givre,...). Elles sont provoquées par un changement de température ou de pression. Les précipitations constituent l’unique « entrée » des principaux systèmes hydrologiques continentaux que sont les bassins versants.
Les processus responsables de la formation des nuages sont décrits dans les manuels de climatologie et leur exposé détaillé sort du cadre de ce cours. Signalons toutefois que la forme, l'ampleur, le développement des nuages dépendent de l'importance et de l'étendue horizontale des mouvements verticaux ascendants qui leur donnent naissance. Quant aux types de nuages, on distingue deux morphologies de base : les nuages stratiformes et cumuliformes. On classe généralement les nuages aussi en fonction de leur altitude : nuages supérieurs, nuages moyens, nuages inférieurs et nuages à développement vertical.


Fig. 3.1 - Exemple de nuages supérieurs (à gauche) et de nuages moyens (à droite) : le cirrus et l'altocumulus (http://www.windows.ucar.edu/)
La formation des précipitations nécessite la condensation de la vapeur d'eau atmosphérique. La saturation est une condition essentielle à tout déclenchement de la condensation. Divers processus thermodynamiques sont susceptibles de réaliser la saturation des particules atmosphériques initialement non saturées et provoquer leur condensation :
La saturation n'est cependant pas une condition suffisante à la condensation ; cette dernière requiert également la présence de noyaux de condensation (impuretés en suspension dans l'atmosphère d'origines variées - suie volcanique, cristaux de sable, cristaux de sel marin, combustions industrielles, pollution) autour desquels les gouttes ou les cristaux se forment. Lorsque les deux conditions sont réunies, la condensation intervient sur les noyaux ; il y a alors apparition de gouttelettes microscopiques qui grossissent à mesure que se poursuit l'ascendance, celle-ci étant le plus souvent la cause génératrice de la saturation. Les noyaux de condensation jouent en faite un rôle de catalyseur pour la formation de gouttelettes d’eau.
Pour qu’il y ait précipitations il faut encore que les gouttelettes ou les cristaux composant les nuages (les hydrométéores) se transforment en gouttes de pluie. Ce phénomène est lié à l'accroissement de ces éléments dont la masse devient suffisante pour vaincre les forces d'agitation. Ce grossissement peut s'expliquer par les deux processus suivant :
Ces explications proviennent essentiellement du site http://zebulon1er.free.fr/pluie.htm qui contient également quelques schémas. Le processus de formation de la pluie est aussi expliqué de manière très pédagogique sur le site http://galileo.cyberscol.qc.ca/InterMet/precipitation/formation_precipitation.htm
Il existe différents types de précipitations : les précipitations convectives, les précipitations orographiques et les précipitations frontales (Fig. 3.2).
Fig. 3.2 - Principaux types de précipitations : convectives, orographiques et frontales
 précipitations convectives. Elles résultent d'une ascension
rapide des masses d'air dans l'atmosphère. Elles sont associées
aux cumulus et cumulo-nimbus, à développement vertical important,
et sont donc générées par le processus de Bergeron. Les
précipitations résultantes de ce processus sont en général
orageuses, de courte durée (moins d'une heure), de forte intensité
et de faible extension spatiale.
précipitations convectives. Elles résultent d'une ascension
rapide des masses d'air dans l'atmosphère. Elles sont associées
aux cumulus et cumulo-nimbus, à développement vertical important,
et sont donc générées par le processus de Bergeron. Les
précipitations résultantes de ce processus sont en général
orageuses, de courte durée (moins d'une heure), de forte intensité
et de faible extension spatiale.
 précipitations orographiques. Comme son nom l'indique (du grec
oros, montagne), ce type de précipitations résulte de la rencontre
entre une masse d’air chaude et humide et une barrière topographique
particulière. Par conséquent, ce type de précipitations
n’est pas « spatialement mobile » et se produit souvent au niveau
des massifs montagneux. Les caractéristiques des précipitations
orographiques dépendent de l'altitude, de la pente et de son orientation,
mais aussi de la distance séparant l'origine de la masse d'air chaud
du lieu de soulèvement. En général, elles présentent
une intensité et une fréquence assez régulières.
précipitations orographiques. Comme son nom l'indique (du grec
oros, montagne), ce type de précipitations résulte de la rencontre
entre une masse d’air chaude et humide et une barrière topographique
particulière. Par conséquent, ce type de précipitations
n’est pas « spatialement mobile » et se produit souvent au niveau
des massifs montagneux. Les caractéristiques des précipitations
orographiques dépendent de l'altitude, de la pente et de son orientation,
mais aussi de la distance séparant l'origine de la masse d'air chaud
du lieu de soulèvement. En général, elles présentent
une intensité et une fréquence assez régulières.
 précipitations
frontales ou de type cyclonique. Elles sont associées aux surfaces
de contact entre deux masses d'air de température, de gradient thermique
vertical, d'humidité et de vitesse de déplacement différents,
que l'on nomme « fronts ». Les fronts froids (une masse d’air
froide pénètre dans une région chaude) créent
des précipitations brèves, peu étendues et intenses.
Du fait d’une faible pente du front, les fronts chauds (une masse d’air chaude
pénètre dans une région occupée par une masse
d’air plus froide) génèrent des précipitations longues,
étendues, mais peu intenses.
précipitations
frontales ou de type cyclonique. Elles sont associées aux surfaces
de contact entre deux masses d'air de température, de gradient thermique
vertical, d'humidité et de vitesse de déplacement différents,
que l'on nomme « fronts ». Les fronts froids (une masse d’air
froide pénètre dans une région chaude) créent
des précipitations brèves, peu étendues et intenses.
Du fait d’une faible pente du front, les fronts chauds (une masse d’air chaude
pénètre dans une région occupée par une masse
d’air plus froide) génèrent des précipitations longues,
étendues, mais peu intenses.En utilisant la seule donnée de précipitation dans une nomenclature climatique, on parvient à définir une répartition mondiale des différents régimes pluviométriques. Pour identifier et classer les diverses régions pluviométriques du globe, on a habituellement recourt aux précipitations moyennes mensuelles ou annuelles (évaluées sur une longue période) et à leurs variations. La précipitation moyenne annuelle établie sur un grand nombre d'année (hauteur moyenne des précipitations annuelles tombant à un endroit donné) est aussi appelée sa valeur normale, son module annuel ou sa valeur inter-annuelle. Une classification pluviométrique générale basée sur les données annuelles est fournie par le tableau suivant.
Tableau 3.1 - Régimes pluviométriques du monde (Tiré de Champoux, Toutant, 1988)
| Nom |
Caractéristiques |
| Régime équatorial humide |
- plus de 200 cm de précipitations annuelles moyennes - à l'intérieur des continents et sur les côtes - région typique de ce régime : bassin de l'Amazone |
| Régime subtropical humide en Amérique |
- entre 100 et 150 cm de précipitation annuelle moyenne - à l'intérieur des continents et sur les côtes - région typique de ce régime : pointe sud-est de l'Amérique du Nord |
| Régime subtropical sec |
- moins de 25 cm de précipitation annuelle moyenne - à l'intérieur des continents et sur les côtes ouest - région typique de ce régime : le sud du Maghreb |
| Régime intertropical sous l'influence des alizés |
- plus de 150 cm de précipitation annuelle moyenne - sur des zones côtières étroites ; humidité - région typique de ce régime : côtes est de l'Amérique centrale |
| Régime continental tempéré |
- entre 10 et 50 cm de précipitation annuelle moyenne - à l'intérieur des continents ; il en résulte des déserts ou des steppes - région typique de ce régime : plaines de l'ouest du continent nord-américain |
| Régime océanique tempéré |
- plus de 100 cm de précipitation annuelle moyenne - sur les côtes ouest des continents - région typique de ce régime : la Colombie britannique, l'Europe |
| Régime polaire et arctique |
- moins de 30 cm de précipitation annuelle moyenne - se situe au nord du 60e parallèle ; formation de grands déserts froids région typique de ce régime : le Grand Nord canadien |
Finalement, les précipitations sont un des processus hydrologiques les plus variables. D'une part, elles sont caractérisées par une grande variabilité dans l'espace et ceci quelle que soit l'échelle spatiale prise en compte (régionale, locale, etc.). D'autre part, elles sont caractérisées par une grande variabilité dans le temps, aussi bien à l'échelle annuelle qu'à celle d'un événement pluvieux
Comme les précipitations varient selon différents facteurs (déplacement de la perturbation, lieu de l'averse, influence de la topographie, etc.), leur mesure est relativement compliquée.
Quelle que soit la forme de la précipitation, liquide ou solide, on mesure la quantité d'eau tombée durant un certain laps de temps. On l'exprime généralement en  hauteur de précipitation ou lame d'eau précipitée par unité de surface horizontale (mm). On définit aussi son
hauteur de précipitation ou lame d'eau précipitée par unité de surface horizontale (mm). On définit aussi son  intensité (mm/h) comme la hauteur d'eau précipitée par unité de temps. La précision de la mesure est au mieux de l'ordre de 0,1 mm. En Suisse, toute précipitation supérieure à 0,5 mm est considérée comme pluie effective.
intensité (mm/h) comme la hauteur d'eau précipitée par unité de temps. La précision de la mesure est au mieux de l'ordre de 0,1 mm. En Suisse, toute précipitation supérieure à 0,5 mm est considérée comme pluie effective.
Les différents instruments permettant la mesure des précipitations sont décrits dans le chapitre 7 "mesures hydrologiques". Citons toutefois les deux appareils de mesures fondamentaux que sont :
 pluviomètre : instrument de base de la mesure des précipitations liquides ou solides. Il indique la quantité d'eau totale précipitée et recueillie à l'intérieur d'une surface calibrée dans un intervalle de temps séparant deux relevés.
pluviomètre : instrument de base de la mesure des précipitations liquides ou solides. Il indique la quantité d'eau totale précipitée et recueillie à l'intérieur d'une surface calibrée dans un intervalle de temps séparant deux relevés.  pluviographe : instrument captant la précipitation de la même manière que le pluviomètre mais avec un dispositif permettant de connaître, outre la hauteur d'eau totale, leur répartition dans le temps, autrement dit les intensités.
pluviographe : instrument captant la précipitation de la même manière que le pluviomètre mais avec un dispositif permettant de connaître, outre la hauteur d'eau totale, leur répartition dans le temps, autrement dit les intensités. Pour un bassin versant donné ou une région donnée, les stations pluviométriques forment un réseau d'observations. Elles fournissent des mesures ponctuelles.
Les données relatives aux stations sont d'une haute importance pour les statistiques climatiques, la planification et la gestion des ressources et les projets de construction ; la nature et la densité des réseaux doivent donc tenir compte du phénomène observé, du but des observations, de la précision désirée, de la topographie, de facteurs économiques ou d'autres encore.
La représentativité des précipitations par les mesures est fonction du réseau d'observation. Plus celui-ci est dense, meilleure est l'information et plus l'ensemble des mesures est représentatif de la lame d'eau tombée sur une surface donnée. Cependant le réseau est le résultat d'un compromis entre la précision désirée et les possibilités ou charges d'exploitation. Le réseau devra donc être planifié. Il existe plusieurs théories sur la planification optimale d'un réseau, mais elles donnent des résultats approximatifs, qui doivent toujours être adaptées aux contraintes locales et financières.
L'hydrologue devra donc faire appel à son expérience de terrain pour planifier un réseau. Il tiendra compte du relief et du type de précipitations (frontales, orographiques, convectives). Il s'assurera également des facilités d'accès, de contrôle et de transmission des informations (par l'homme ou par télétransmission : téléphone, satellite, etc.).
La publication des données pluviométriques est du ressort des services publics (en Suisse et à l'échelle nationale, l'Institut Suisse de Météorologie) qui le font généralement sous forme d'annuaires. En Suisse, la publication de référence s'intitule "Ergebnisse der täglichen Niederschlagen" (résultats des mesures de précipitations journalières). Les annuaires pluviométriques regroupent, pour chacune des stations de mesure, les résultats suivants :
Un certain nombre de ces grandeurs est accessible en temps réel par le biais du site Internet de l'Institut Suisse de Météorologie (http://www.meteosuisse.ch/fr/). Il est alors possible de consulter l'évolution et la répartition spatiale de plusieurs paramètres hydroclimatiques.
Certaines de ces valeurs peuvent être régionalisées et présentées sous forme de cartes d'isohyètes (cartes d'équivaleurs de précipitations). Il existe d'autres ouvrages de synthèse qui sont davantage dirigés vers une analyse synthétique des précipitations (exemple de l'«Atlas hydrologique de la Suisse» http://hydrant.unibe.ch/hades/hades_fr.htm).
Les  mesures ponctuelles acquises au niveau des pluviomètres ou des pluviographes sont analysées et soumises à différents traitements statistiques.
mesures ponctuelles acquises au niveau des pluviomètres ou des pluviographes sont analysées et soumises à différents traitements statistiques.
On désigne en général par "averse" un ensemble de pluies associé à une perturbation météorologique bien définie. La durée d'une averse peut donc varier de quelques minutes à une centaine d'heures et intéresser une superficie allant de quelques kilomètres carrés (orages) à quelques milliers (pluies cycloniques). On définit finalement une averse comme un épisode pluvieux continu, pouvant avoir plusieurs pointes d'intensité. L'intensité moyenne d'une averse s'exprime par le rapport entre la hauteur de pluie observée et la durée t de l'averse :
| (3.1) |
Où :
im : intensité moyenne de la pluie [mm/h, mm/min]
ou ramenée à la surface [l/s.ha],
h : hauteur de pluie de l'averse [mm],
t : durée de l'averse [h ou min].
L'intensité des précipitations varie à chaque instant au cours d'une même averse suivant les caractéristiques météorologiques de celle-ci. Plutôt que de considérer l'averse entière et son intensité moyenne, on peut s'intéresser aux intensités observées sur des intervalles de temps au cours desquels on aura enregistré la plus grande hauteur de pluie. On parle alors d'intensité maximale.
Deux types de courbes déduites des enregistrements d'un pluviographe (pluviogramme) permettent d'analyser les averses d'une station :
La courbe des hauteurs de pluie cumulées représente en ordonnée, pour chaque instant t, l'intégrale de la hauteur de pluie tombée depuis le début de l'averse.
Le  hyétogramme
est la représentation, sous la forme d'un histogramme, de l'intensité
de la pluie en fonction du temps. Il représente la dérivée
en un point donné, par rapport au temps, de la courbe des précipitations
cumulées. Les éléments importants d'un hyétogramme
sont le pas de temps Dt et sa forme.
Communément, on choisit le plus petit pas de temps possible selon la
capacité des instruments de mesure. Quant à la forme du hyétogramme,
elle est en général caractéristique du type de l'averse
et varie donc d'un événement à un autre.
hyétogramme
est la représentation, sous la forme d'un histogramme, de l'intensité
de la pluie en fonction du temps. Il représente la dérivée
en un point donné, par rapport au temps, de la courbe des précipitations
cumulées. Les éléments importants d'un hyétogramme
sont le pas de temps Dt et sa forme.
Communément, on choisit le plus petit pas de temps possible selon la
capacité des instruments de mesure. Quant à la forme du hyétogramme,
elle est en général caractéristique du type de l'averse
et varie donc d'un événement à un autre.

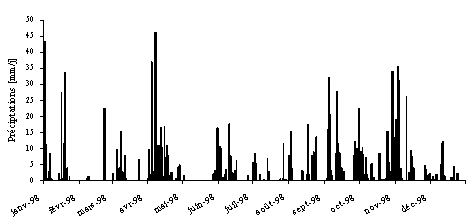
Fig. 3.3 - Courbe des pluies cumulées et hyétogramme.
Le critère de continuité d'un épisode pluvieux varie selon le bassin versant. Généralement, deux averses sont considérées comme distinctes : (1) si la précipitation DH tombant durant l'intervalle de temps Dt qui les sépare est inférieure à un certain seuil et (2) si cet intervalle de temps est lui-même supérieur à une certaine valeur définie compte tenu du type de problème étudié. En représentant les averses sous forme de hyétogrammes, la problématique de la séparation des averses se résume comme suit (figure 3.4) :
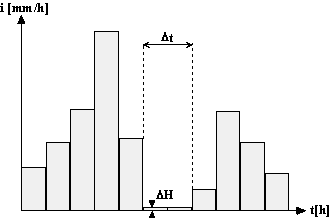
Fig. 3.4 - Conditions pour la distinction de deux averses consécutives (1) DH durant Dt < seuil (par exemple 2 mm) et (2) Dt > durée choisie en fonction du problème (par exemple 1 heure)
Cette notion d'averse est très importante en milieu urbain et de petits bassins versants car elle s'avère déterminante pour l'estimation des débits de crue.
L'ensemble des données d'une station de mesures pluviométriques constitue une information considérable qu'il est souhaitable de condenser à l'aide de caractéristiques bien choisies. On applique ainsi les lois et d'autres techniques de la statistique aux relevés pluviométriques pour en tirer des informations utiles aux études et travaux envisagés. On détermine de la sorte :
L'ensemble de ces valeurs ponctuelles, condensées sous forme statistique, est utilisé pour déterminer la fréquence et les caractéristiques d'un événement pluvieux isolé ou encore pour étudier la variabilité de la pluviométrie dans l'espace.
Les projets d'aménagements hydrauliques ou hydrologiques sont souvent définis par rapport à une averse type associée aux fréquences probables d'apparition.
Lorsque l'on étudie des grandeurs comme les précipitations (caractérisées à la fois par leur hauteur et leur durée) ou les débits de crue d'un point de vue statistique, on cherche donc et, en règle générale, à déterminer par exemple la probabilité pour qu'une intensité i ne soit pas atteinte ou dépassée (i.e. soit inférieure ou égale à une valeur xi).
Cette probabilité est donnée, si i représente une variable aléatoire, par la relation suivante :
| (3.2) |
On nomme cette probabilité fréquence de non-dépassement ou probabilité de non-dépassement. Son complément à l'unité 1- F(xi) est appelé probabilité de dépassement, fréquence de dépassement ou encore fréquence d'apparition.
On définit alors le  temps
de retour T d'un événement comme étant l'inverse
de la fréquence d'apparition de l'événement. Soit :
temps
de retour T d'un événement comme étant l'inverse
de la fréquence d'apparition de l'événement. Soit :
| (3.3) |
Ainsi, l'intensité d'une pluie de temps de retour T est l'intensité qui sera dépassé en moyenne toutes les T années.
Si l'analyse fréquentielle d'une série d'intensités maximales de pluie permet de déterminer le temps de retour d'une valeur particulière il n'est en revanche et a priori pas possible de répondre à d'autres questions pertinentes qui peuvent se poser à l'ingénieur. Par exemple, la notion de temps de retour ne permet pas de répondre aux questions où q est la probabilité que l'événement ne se produise pas dans une année en particulier. Pour plus d'informations sur l'analyse fréquentielle, consultez cet annexe
Une pluie peut être caractérisée par plusieurs paramètres qui peuvent avoir, au sein de la même pluie, des temps de retour très différents. Citons notamment :
L'analyse des pluies a permis de définir deux lois générales de pluviosité qui peuvent s'exprimer de la manière suivante :
Ces lois permettant d'établir les relations entre les
intensités, la durée et la fréquence d'apparition des pluies
peuvent être représentées selon des courbes caractéristiques :
on parle généralement de  courbes
Intensité-Durée-Fréquence (IDF) (Fig. 3.5).
La notion de fréquence est en faite exprimée par la notion
de temps de retour.
courbes
Intensité-Durée-Fréquence (IDF) (Fig. 3.5).
La notion de fréquence est en faite exprimée par la notion
de temps de retour.
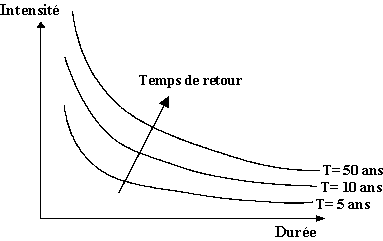
Fig. 3.5 - Représentation schématique des courbes IDF
Les courbes IDF ne sont pas une fin en soi, mais sont construites dans un but bien précis. Elles permettent d'une part de synthétiser l'information pluviométrique au droit d'une station donnée et, d'autre part de calculer succinctement des débits de projet et d'estimer des débits de crue ainsi que de déterminer des pluies de projet utilisées en modélisation hydrologique.
Les courbes IDF sont établies sur la base de l'analyse d'averses enregistrées à une station au cours d'une longue période. Les courbes obtenues peuvent donc être construites de manière analytique ou statistique.
Différentes formules sont proposées pour représenter l'intensité critique d'une pluie en fonction de sa durée.
La forme la plus générale (avec T variable) est la suivante :
| (3.4) |
Avec :
i : intensité totale [mm/h], [mm/min] ou intensité spécifique
[l/s.ha],
T : période de retour en années,
t : durée de référence [h ] ou [min],
k, a, b, c : paramètres d'ajustement.
Montana suggère une formulation plus simple :
| (3.5) |
Avec :
i: intensité maximale de la pluie [mm/h],
t: durée de la pluie [minutes ou heures],
T; intervalle de récurrence (ou temps de retour) [années],
a,b: constantes locales, dépendant généralement du lieu (0.3<0.8).Pour une fréquence de dépassement donnée, cette formule de Montana a été adaptée pour la Suisse et a abouti à la formulation suivante (Bürki et Ziegler, 1878) :
| (3.6) |
où a est une constante définie localement et qui varie selon le lieu géographique de l'observation.
La figure 3.6 (a, b et c) représente les courbes IDF, calculées pour les différentes régions de la Suisse qui figurent dans les normes suisses pour la construction routière (Norme Suisse SNV 640-350 p 5). Les courbes sont présentées selon un découpage suisse en zones d’égale intensité, et un tableau dans lequel figurent les valeurs de K en fonction du temps de retour, ainsi que les valeurs de B pour ces différentes zones. Elles s'expriment par :
| (3.7) |
Où :
r : intensité spécifique moyenne d'une pluie d'une durée de t minutes atteinte ou dépassée en moyenne une fois toutes les T années [l/s/ha],
K : coefficient fonction du lieu et du temps de retour et B une constante de lieu [min].
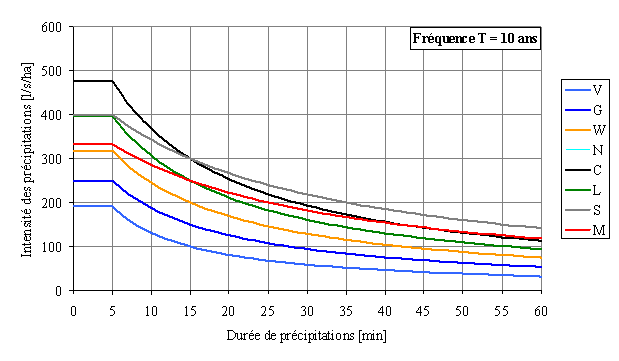
Fig. 3.6.a - Courbes IDF pour les différentes régions de la Suisse, déterminées par l'EAWAG
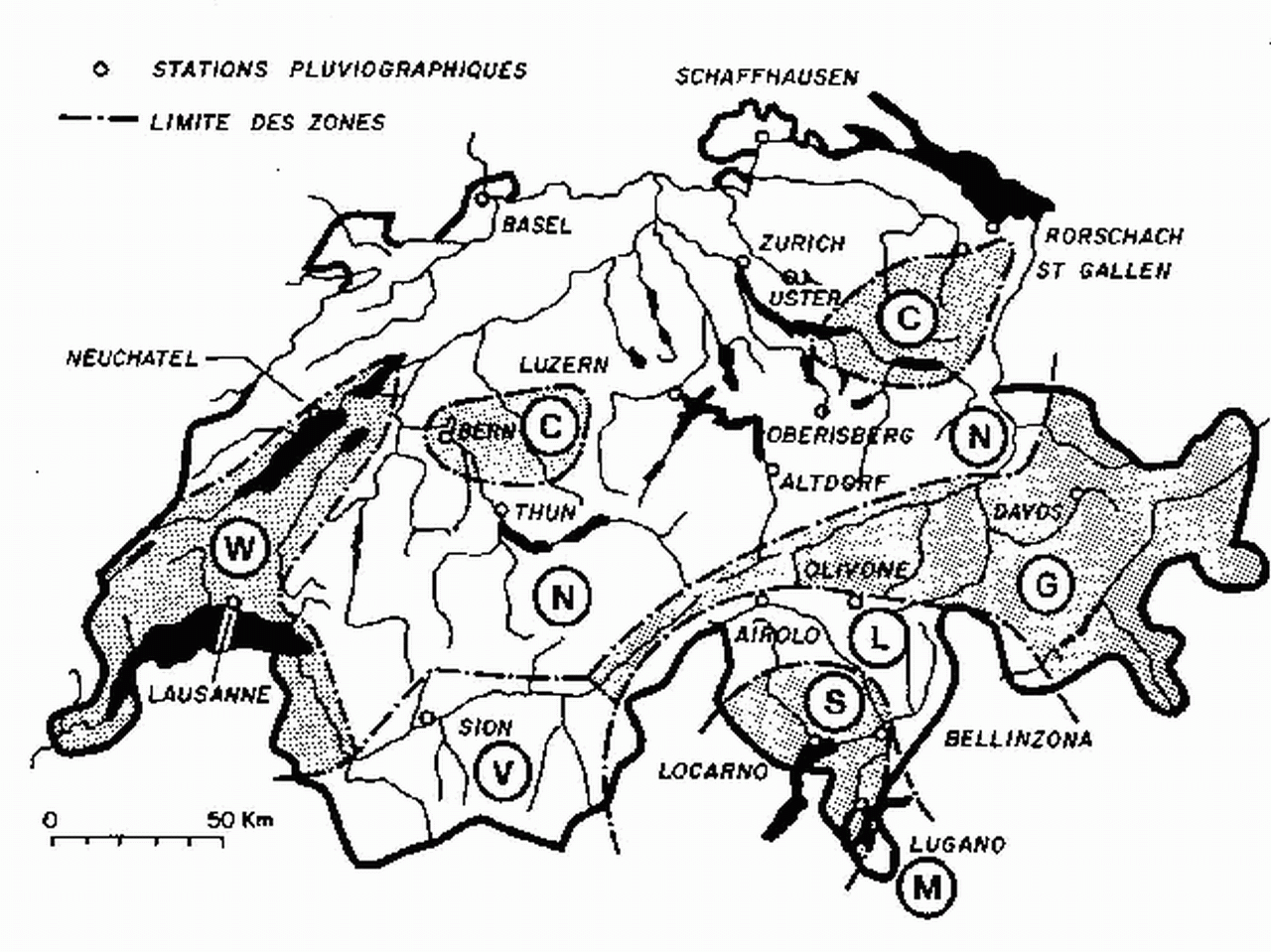
Fig. 3.6 b. - Délimitation des zones d’intensité égale pour la Suisse (SNV 640-350)
| |
Valeur de K selon le temps de retour compris entre 1 et
20 ans |
B |
||||||
|
Zone |
Sur la carte |
1 |
2 |
5 |
10 |
15 |
20 |
|
|
Alpes |
|
|
|
|
|
|
|
|
|
Valais |
V |
1050 |
1350 |
1700 |
2100 |
2300 |
2400 |
6 |
|
Grisons |
G |
1900 |
2450 |
3000 |
3750 |
4100 |
4300 |
10 |
|
Nord des Alpes |
|
|
|
|
|
|
|
|
|
Ouest |
W |
2700 |
3500 |
4300 |
5400 |
5950 |
6200 |
12 |
|
Nord-est |
N |
3400 |
4400 |
5400 |
6750 |
7450 |
7750 |
12 |
|
Centre |
C |
4050 |
5250 |
6500 |
8100 |
8900 |
9300 |
12 |
|
Sud des Alpes |
|
|
|
|
|
|
|
|
|
Léventina |
L |
3400 |
4400 |
5400 |
6750 |
7450 |
7750 |
12 |
|
Sotto-Sopra
Ceneri |
S |
6000 |
7800 |
9600 |
12000 |
13200 |
13800 |
25 |
|
Mendrisiotto |
M |
5000 |
6500 |
8000 |
10000 |
11000 |
11500 |
25 |
Fig. 3.6.c. - Tableau des coefficients K et B utilisées dans les calculs des courbes IDF selon la norme SNV
2. Représentation statistique
Les courbes IDF sont établies sur la base de l'analyse d'averses enregistrées à une station au cours d'une longue période. L'analyse fréquentielle peut s'appliquer si on ne présuppose pas une loi connue (de type Montana, etc.) et si on s'intéresse à des événements rares, donc extrêmes. Les données recueillies sont alors ajustées, à un pas de temps choisi, à une loi statistique qui doit décrire relativement bien la répartition des extrêmes. La loi de Gumbel est la plus utilisée. Si l'opération est répétée sur plusieurs pas de temps, on obtient la variation de l'intensité avec la durée de la pluie pour différents temps de retour, c'est à dire des courbes IDF de la station considérée sur la période analysée.
La structure d'une averse est définie comme la distribution de la hauteur de pluie dans le temps. Cette distribution influence de manière notoire le comportement hydrologique du bassin versant.
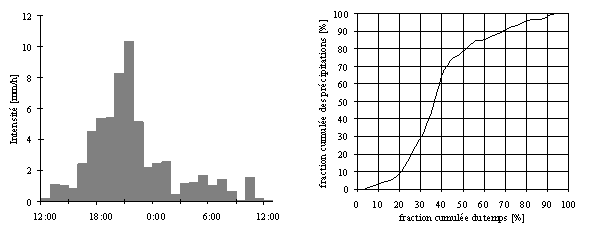
Fig. 3.7 Exemple de hyétogramme et de structure correspondante pour une précipitation enregistrée au nord de Lausanne du 13 novembre 1991 à 12h00 au 14 novembre à 12h00
Le passage des mesures ponctuelles des précipitations à une estimation spatiale de celles-ci, souvent nécessaire en hydrologie, est délicat. Les méthodes les plus simples et les plus couramment utilisées sont les méthodes de calcul de moyennes ou les méthodes d'interpolation des données pluviométriques collectées localement. Ces méthodes permettent notamment le calcul des lames d'eau moyennes à l'échelle du bassin, la cartographie des précipitations, et le calcul de hyétogrammes moyens. Des méthodes faisant appel à la notion d'abattement des pluies existent également.
Avant de procéder au calcul de la précipitation moyenne du bassin versant, il importe de contrôler la qualité des données pluviométriques, leur homogénéité et leur représentativité (cf. chapitre "le contrôle des données").
Parmi les méthodes généralement proposées
pour calculer la  moyenne
des pluies à partir de l'ensemble des mesures ponctuelles obtenues
à plusieurs stations pluviométriques sur le bassin ou à
proximité, on distingue la méthode de la moyenne arithmétique,
la méthode des polygones de Thiessen ou l'utilisation d'isohyètes.
Le choix de la méthode dépendra notamment de la longueur de la
série de données dont on dispose, la densité du réseau
de mesure, et la variation du champ pluviométrique.
moyenne
des pluies à partir de l'ensemble des mesures ponctuelles obtenues
à plusieurs stations pluviométriques sur le bassin ou à
proximité, on distingue la méthode de la moyenne arithmétique,
la méthode des polygones de Thiessen ou l'utilisation d'isohyètes.
Le choix de la méthode dépendra notamment de la longueur de la
série de données dont on dispose, la densité du réseau
de mesure, et la variation du champ pluviométrique.
La méthode la plus simple qui consiste à calculer la moyenne arithmétique des valeurs obtenues aux stations étudiées, s'applique uniquement si les stations sont bien réparties et si le relief du bassin est homogène.
Cette méthode est souvent peu recommandée car peu représentative. Il faut lui préférer des méthodes graphiques (tracé d'isohyètes) ou statistiques qui permettent de donner un poids différent à chacun des points de mesures (moyennes pondérées).
La méthode du  polygone
de Thiessen est la plus couramment utilisée, parce que son application
est aisée et qu'elle donne en général de bons résultats.
Elle convient notamment quand le réseau pluviométrique n'est pas
homogène spatialement (pluviomètres distribués irrégulièrement).
polygone
de Thiessen est la plus couramment utilisée, parce que son application
est aisée et qu'elle donne en général de bons résultats.
Elle convient notamment quand le réseau pluviométrique n'est pas
homogène spatialement (pluviomètres distribués irrégulièrement).
Cette méthode permet d'estimer des valeurs pondérées en prenant en considération chaque station pluviométrique. Elle affecte à chaque pluviomètre une zone d'influence dont l'aire, exprimée en %, représente le facteur de pondération de la valeur locale. Les différentes zones d'influence sont déterminées par découpage géométrique du bassin sur une carte topographique 1 (voir figure 3.8). La précipitation moyenne pondérée Pmoy pour le bassin, se calcule alors en effectuant la somme des précipitations Pi de chaque station, multipliées par leur facteur de pondération (aire Ai), le tout divisé par la surface totale A du bassin. La précipitation moyenne sur le bassin s'écrit :
| (3.8) |
Avec :
Pmoy : précipitation moyenne sur le bassin,
A : aire totale du bassin (=å Ai),Pi :
précipitation enregistrée à la station i,
Ai : superficie du polygone associée à la
station i.
Fig. 3.8 - Exemple de détermination des polygones de Thiessen (vous pouvez changer les valeurs de pluie ponctuelle et calculer la pluie moyenne).
1Les stations disponibles étant reportées sur une carte géographique, on trace une série de segments de droites reliant les stations adjacentes. On élève des perpendiculaires au centre de chacune des droites (médiatrices); les intersections de ces perpendiculaires déterminent des polygones. Dans chaque polygone, la hauteur de précipitation choisie est celle relevée à la station située à l'intérieur de celui-ci. Les côtés des polygones et/ou la ligne de partage des eaux représentent les limites de l'aire (et du poids) accordée à chaque station. L'aire de chaque polygone Ai est déterminée par planimétrie ou numériquement. D'autres critères pour la détermination des valeurs de pondération peuvent être adoptés. Ceux-ci peuvent être fonction de l'averse, du relief, de la position géographique, etc.
La méthode la plus rigoureuse mais qui présente l'inconvénient de demeurer lourde en dépit des moyens actuels, est fondée sur l'utilisation des isohyètes.
Les  isohyètes sont des lignes de même pluviosité (isovaleurs
de pluies annuelles, mensuelles, journalières, etc.). Grâce aux
valeurs pluviométriques acquises aux stations du bassin et aux autres
stations avoisinantes, on peut tracer le réseau d'isohyètes. Le
tracé des isohyètes n'est pas unique comme celui des courbes de
niveau. Il doit être dessiné avec le maximum de vraisemblance compte
tenu de la région, du réseau, de la qualité de la mesure,
etc. Il existe aujourd'hui des méthodes automatiques qui effectuent le
tracé d'isovaleurs par des moyens statistiques élaborés
(technique de krigeage).
isohyètes sont des lignes de même pluviosité (isovaleurs
de pluies annuelles, mensuelles, journalières, etc.). Grâce aux
valeurs pluviométriques acquises aux stations du bassin et aux autres
stations avoisinantes, on peut tracer le réseau d'isohyètes. Le
tracé des isohyètes n'est pas unique comme celui des courbes de
niveau. Il doit être dessiné avec le maximum de vraisemblance compte
tenu de la région, du réseau, de la qualité de la mesure,
etc. Il existe aujourd'hui des méthodes automatiques qui effectuent le
tracé d'isovaleurs par des moyens statistiques élaborés
(technique de krigeage).
Lorsque les courbes isohyètes sont tracées, la pluie moyenne peut être calculée de la manière suivante :
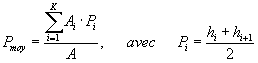 |
(3.9) |
Avec :
Pmoy : précipitation moyenne sur le bassin,
A : surface totale du bassin,
Ai : surface entre deux isohyètes i et i+1,
K : nombre total d'isohyètes,
Pi : moyenne des hauteurs h de précipitations entre
deux isohyètes i et i+1.
Le calcul du hyétogramme moyen permet de connaître la quantité mais surtout la distribution temporelle de la précipitation pour un événement pluvieux sur un bassin versant donné, même s'il est dépourvu d'enregistrements pluviographiques.
Le calcul se fait selon les étapes suivantes :
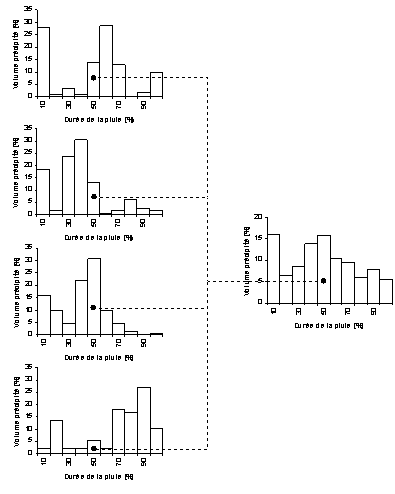
Fig. 3.9 - Exemple d'un hyétogramme moyen.
Dans de nombreuses études hydrologiques, il est nécessaire
de connaître la lame d'eau précipitée sur le bassin versant.
Un des moyens permettant l'estimation d'une lame d'eau à partir d'une
hauteur de pluie ponctuelle tout en tenant compte de l'hétérogénéité
des précipitations est l'utilisation d'un  coefficient
d'abattement ou de réduction.
coefficient
d'abattement ou de réduction.
De nombreuses définitions différentes de coefficients d'abattement existent.
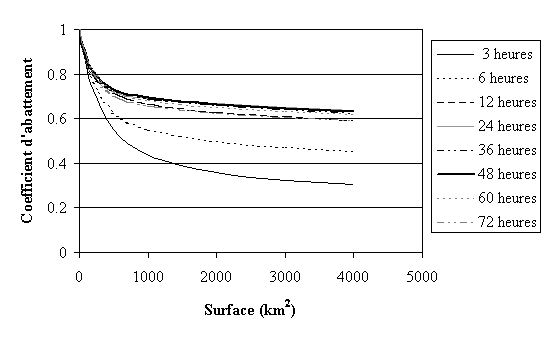
Fig. 3.10 - Exemple de coefficient de réduction des hauteurs de précipitations régionales en fonction de la durée des précipitations et de la surface considérée (d'après les données de l'Atlas hydrologique de la Suisse, zone 1).
| (3.10) |
Avec :
K : coefficient d'abattement,
Pm : pluie moyenne sur la surface, de fréquence donnée,
P : pluie ponctuelle de même probabilité.Cette définition implique qu'en chaque point, la pluie suit une même loi de probabilité. Cette condition d'isotropisme de la pluie sur la surface est assez bien respectée pour une région homogène et peut s'appliquer dans le cas de petits bassins versants.